Introduction

 

The intersection between physical laws and fundamental constants is what we know, it is what we experience, it is in turn the basis for our understanding of the created order. This understanding is nothing short of a blessed revelation by God. It is grace. And what a revelation it is, to thus be granted a peek into His amazing handiwork (it is a peek just now, the full panorama comes later). So,

 

(1)    What exactly, or where exactly, is that intersection and,

(2)    why is it a basis for our understanding of the created order?

 

(1)    It is that hyper-fine, hyper-fragile threshold where abstraction melds into mundane reality. To be clear, mundane reality is our reality, it is not quintessential reality, which is God’s reality, which is Truth. Mundane reality is a subset of God’s reality.

(2)    It is a basis because the created order must be understood according to what it actually is, namely, the reality we perceive and experience all around us in myriad ways.

 

Thus do the physical laws and fundamental constants intersect at that amazing threshold to reveal an aspect of God’s reality, a particular truth in the dress of mundane reality. With God’s help and guidance, we hope to expound on this below.

 

Physical laws describe the behavior of the created order. They are comprised of and express relationships, relationships between forces and phenomena and quantities per se. These laws can be stated, that is, simply spoken. For example, phenomenon A always does thus and so gently and slowly for seven seconds at which time it is spent; phenomenon B always does thus and so robustly and near instantly with respect to phenomenon C; energy can never be created or destroyed, it can only be transformed from one form to another, and the total energy of a system plus its surroundings remains constant (first law of thermodynamics), and so on. Or these laws can be stated mathematically—a different kind of “speak.” For example, deltaU= Q-W (first law of thermodynamics—change in internal energy U of system = heat Q supplied to system minus work W done by system); electric field E = k q/r^2 (Coulomb’s law for the electric field, thus the electric force between charge q shown and another charge say q1 equals q1 E, that is, there is a precise mathematical relationship between electric field and electric force, and electric potential as well). These relationships we exploit to simplify and streamline our computations; in this way we peel back the layers of the created order by way of relationships inherent in and between physical laws. Now, fundamental constants appear in these laws as coefficients or scaling factors. For example, the “q” in Coulomb’s law for the electric field mentioned is a scaling factor, it is a fundamental constant, it is the electric charge, whose scaling effect is discrete because q increments in integer multiples of elementary charge q, reflecting the quantized nature of electric charge (elementary charge q approximately equals 1.602 10^-19 coulombs, so we can have say -2q, -1q, 0, 1q, 2q, and so on). Fundamental constants provide the numerical values that make the abstract physical laws applicable to our mundane reality. That is very important. In the red font text lies the sought after intersection between physical laws and fundamental constants—said intersection is in fact that mundane reality. Put another way, the fundamental constants ground mathematical abstractions in mundane reality. We are after numbers here, established by measurements, which are themselves grounded in mundane reality. Moreover, fundamental constants ensure dimensional consistency in equations. Physical laws must have consistent units, and the constants provide the necessary conversions. For example, the speed of light “c” (a fundamental constant) ensures that energy and mass are related consistently in the mass-energy physical law (energy_rest = mass_rest c^2 where we have for the energy kilogram meter^2/second^2, so to balance with mass in kilograms, we need c^2 which is meter^2/second^2 mutltiplying the mass). Please note: God’s fine-tuning of His universe involves the precise values of fundamental constants. That is why we enjoy a stable reality in this universe He gave us which we call home. If these constants were slightly different than God’s precisely determined values, life as we know it would not exist in the first place, and even if it did somehow, impossible though that would be, it could not survive given an unstable reality within which it would find itself. So, physical laws in the language of mathematics describe how the universe behaves, and fundamental constants provide the numerical framework for those laws. Together, they shape our understanding of mundane reality. One wonders,

 

(1)    Where does this laws<>constants marriage, this mathematics, come from and,

(2)    why does it precisely quantify mundane reality so well?

 

(1)    Mathematics comes from, it emerges, foremost from human curiosity, a serious bent to understand our mundane reality, which leads to keen observation of that reality, and then follows pattern recognition—and from that comes mathematical abstraction. (In Genesis 1:26-28 the command to “subdue” and “rule over” the creation relates to our innate curiosity, our capacity for observation, and ultimately our use of mathematics to understand and manage the world around us—we are thus “wired” and equipped by God precisely because we are created in His image.) In short, we have:

 

curiosity driven observation+pattern recognition-> mathematical abstraction.

 

One could say that observation of mundane reality leads to mathematical formulation of that reality. It presupposes that some manner of reality is available for observation a priori. Reality is what it is, and mathematics is simply an abstraction of that reality. It is intuitively obvious that mathematics is not the reality that it abstracts.

 

(2)    Mathematics quantifies mundane reality very precisely because it computes—obviously we need some means to compute to be able to quantify anything; computation inherently involves quantification and vice versa. But there is more to it than that. Importantly, our mathematics computes in the very language that the universe expresses itself in. If it weren’t so, we could not possibly realize the precision in our computations that we do. Not to say that the picture is complete, there’s a lot to that universe-language yet to be learned, but so far so good thanks to God’s revelatory grace down through the centuries. We praise you Lord for your amazing handiwork and thank you for your revelatory grace. Amen.

 

Okay, well and good, but what about purely mathematical constants? How do purely mathematical constants fit into the overall discussion of physical laws and their associated fundamental constants? It’s a little different. And where is the reality intersection in this case, or is there one? Yes, there is. That is where we are going in this study—purely mathematical constants and their (mundane) reality intersection. We are going to engage this purely mathematical constants angle via the “Dream Team” of numbers. In the order of increasing value we have:

 

i (the imaginary unit), 0 (the additive identity), 1 (the multiplicative identity), e (the transcendental Euler’s number), and pi (the transcendental Archimedes’ constant {i, 0, 1, e, pi}—“Dream Team” henceforth, with respective values {-1^1/2, 0, 1, 2.71828…, 3.1415…}. (Transcendental means non-algebraic/non-polynomial in the sense that a transcendental number cannot be expressed as the solution to an algebraic equation with integer coefficients.)

 

There are other constants, certainly plenty of physical ones, that deserve mentioning in this elite class, but only these five purely mathematical ones interest us in this study. The Dream Team members are themselves generalizations, a coming together of centuries of human inquiry satisfied by humankind’s quite unique, God-given associative skills tempered by no less unique, God-given human ingenuity. They interest us because they form the bedrock of our mathematical understanding, and our physical laws from the simplest to the most complex are for the most part rubbish without them.

 

The Imaginary Unit (i), Imaginary Numbers

 

Background

 

An imaginary number is the product of a real number and the imaginary unit, the latter being the square root of negative 1, which is decidedly imaginary—any number squared can never yield a negative result; “unit” is utilized in this instance because “1” is considered. As far as we know, the mathematician Hero(n) of Alexandria was maybe the first to do calculations involving the square root of negative numbers, but it was Girolamo Cardano who is credited with introducing negative and imaginary numbers in his treatise “Ars Magna” (The Great Art) in the middle of the sixteenth century. He discussed these concepts, but they were not widely accepted at the time. Rafael Bombelli near the end of the sixteenth century first developed and established the rules for multiplying numbers involving the imaginary unit. His work laid the groundwork for understanding imaginary numbers. Leonhard Euler (18th century), certainly one of the greatest mathematicians of all time, introduced the notation “i” for the imaginary unit and demonstrated its surpassing usefulness in solving mathematical problems. Euler’s work significantly contributed to the acceptance of imaginary numbers. Carl Friedrich Gauss (early 19th century), another of the great mathematicians on the human plane, if not the greatest of all time, greatly developed the theory of complex numbers which consist in part of imaginary numbers, emphasizing their geometric interpretation. He showed that complex numbers could be represented as points in a plane, which led to the concept of the complex plane. In that regard Caspar Wessel (1745–1818) described the geometric significance of complex numbers as points in a plane, emphasizing their relationship to real and imaginary components (while Gauss made significant contributions to the understanding of complex numbers, Wessel’s geometrical interpretation paved the way for visualizing them in the complex plane. Their combined efforts contributed to our understanding of complex numbers and their rich mathematical utility). Bottom line, the concept of imaginary numbers and ultimately complex numbers came together gradually, with contributions from various mathematicians. Initially regarded as quite fictitious or useless, these numbers gained acceptance particularly due to the efforts of Euler, Gauss, and Wessel, and others to be sure. Today, imaginary numbers play a crucial role in engineering, mathematics, and physics, allowing us to understand phenomena beyond the real number line. A little more on their geometric interpretation. We want to “build” a simple geometry here, because the simpler it is upfront, the easier it is to compute with later. It is essential in math and physics, the sciences per se, to keep things as simple as possible for as long as possible. And to do so in this context, we consider one of the simplest geometric objects available to us—a two-dimensional (2D) plane. We begin building this geometry via a couple of axes intersecting perpendicularly. Now extend both axes to +/- infinity— a massive plane is the result. Next, we need granularity in that plane, because without that, we cannot address the detail inherent in our problems—ultimately, we want to grace our computations with detail (we are anticipating real world problems that are not so simple, but we are going to try to simplify them by translating them onto our very simple “geometry” that we are constructing). So, we need granularity, and we achieve this by imagining our plane being sliced vertically and horizontally many times, always parallel to the vertical axis for the vertical slices and parallel to the horizontal axis for the horizontal slices. When this slicing is imagined in the mind’s eye, we see myriad intersection points—places where the slices intersect—and those intersection points comprise our granular “complex number plane” as it is called. So, the 2D complex number plane is comprised of two perpendicular axes, one horizontal representing the “real” axis, and the other vertical, representing the “imaginary” axis and a crisscross of perpendicular slices giving rise to “grains” (Fig. 1). This is our simple geometric picture which we will exploit by placing complicated and difficult real-world problems onto this complex number plane “grid,” but to do what? To make “measurements.” We will describe distances and rotations, forces and phenomena and whatnot, by way of this complex number plane “ruler,” or “metric” as it is called. Let’s do a concrete example. Consider a complex number of the form (a + bi), where the factor a scales the horizontal, real number line or axis, and the factor b scales the vertical, imaginary axis. Now, each complex number corresponds to a point {a, b} in the complex plane (“point” = “grain” of granularity mentioned above; one of our “grains” is in fact a complex number). For example, the complex number, say, 4-2i corresponds to the point {a=4, b=-2} in the complex plane—it is the “grain” {4,-2} in the complex plane; we are at a precise location in the complex number plane (Fig. 2). Here is where it gets interesting and practical. A complex number packs a lot of information. It succinctly gives information about the modulus and orientation of the object it represents. In this example, the modulus is Sqrt[4^2+(-2)^2]= Sqrt[20] = 2 Sqrt[5] or about 4.47, which is the underlying object’s straight line distance from the black grain at {0,0} to the red grain at {4,-2}, and it gives information about the orientation of this object relative to the positive real axis. We have Tangent[angle]= imaginary/real. In this example we get Tangent[angle] =-2/4, thus angle =ArcTan[-1/2], which is about -26.6 degrees. This represents a rotation of 26.6 degrees clockwise from the positive real axis around and over to the red square (negative angles are measured clockwise from the positive real axis in the complex plane). But perhaps the real wonder of complex numbers is that they extend our understanding beyond the real number line; they can be used to help model anything that rotates and/or extends between the two dimensions represented by our axes, and we are free to let the axes represent elements of our real-world problem. These dimensions via the complex plane allow us to work with quantities that do not have a direct physical interpretation. While real numbers describe measurable quantities (like distance, temperature, or time), imaginary numbers represent abstract relationships, such as rotations, oscillations, and waves. To be clear with the terminology, imaginary numbers are a subset of complex numbers; while all imaginary numbers are complex, not all complex numbers are purely imaginary. For example, -2i is purely imaginary because it has no real part, 4-2i is a bit more complex—please forgive the pun—because it has a real and an imaginary part. Imaginary numbers, whether purely imaginary or not, bridge the gap between the tangible and the conceptual. They emerge naturally when solving equations that involve square roots of negative numbers—this inevitably happens sometimes in problem-solving that one ends up with such a quadratic equation. For instance, suppose some problem gave rise to the quadratic equation x^2 + 1 = 0; the solutions are x = +/- i, where i is the imaginary unit (-1^1/2). These sorts of imaginary solutions, then, urge us to work with complex numbers when expressing problems that give rise to imaginary solutions, oftentimes to the unraveling of an otherwise unsolvable problem. Euler’s formula e^(i theta) = Cos[theta] + i Sin[theta] is important in this context, it brings together real and imaginary components, and it connects exponential functions with trigonometry (the unit circle in the complex plane traces out these relationships as theta varies). These are some of the reasons why Imaginary numbers play a crucial role in fields like electrical engineering, quantum mechanics, in particular quantum wave functions, and signal processing/AC circuits, which all rely on the ubiquitous Fourier transform and its complex number plane conceptualization (the Fourier transform seemingly shows up everywhere in the created order—an oft used assembly-level computation by God). Without imaginary numbers, our understanding of the phenomena these fields abstract would be incomplete. It goes without saying that imaginary numbers are quite ingenious, they enrich our mathematical language, empower problem-solving, and unlock hidden patterns in the universe (recall that at the heart of mathematics and, once removed, the sciences, lies observation and pattern recognition). So, just as negative numbers per se were once considered absurd but later became essential, complex numbers with their real and imaginary components have their own unique place in mathematics and the math-intensive sciences. They’re not just abstractions; they help us explore dimensions beyond what the real numbers can offer us.

 

We have given the bare-bone basics here, much, much more could be said regarding applications, the geometric interpretation, and the developmental history. Our goal was to introduce the imaginary unit, sort of describe what it is, how it came about, and stress its crucial role in real-world problem solving. We will meet this Dream Team member again when we discuss its teammate “e.”

 

Reality intersection

 

Before we discuss this topic with all these numbers, starting with this one, it must be said that Jesus Christ is that Intersection first and foremost (John 1:1-3, Colossians 1:15-17). No number, no matter how “dreamy,” can reveal what Jesus reveals about Reality. Jesus Christ of Himself is quintessential Reality because He is in fact God’s Reality, which we can appreciate and experience through His Word and by personal relationship with Him, respectively. That said, let’s come down off the mountaintop a bit and think about this intersection in the context of very mundane imaginary numbers. As said above in a red font, they bridge the gap between the tangible and the conceptual—we will consider that to be our mundane reality intersection. These numbers emerge as solutions to equations that have no real roots (roots are values that satisfy/solve a specific equation), but there are roots, imaginary ones. Now, equations are truth relations—something is equal to this other thing or maybe not—a truth relationship test. Like a teeter-totter tipping one way or another or maybe level, i.e., a balance, a truism. If a truth relationship (equation) stemming from a real-world problem has no real roots, and yet the problem is obviously quite real, it is necessary therefore that something relates that underlying reality, after all, there is an underlying reality that gave rise to the equations. There seems to be a “gap” as it were, between what is known to be real, and the qualifying and quantifying computation that gave imaginary roots as representative of that reality. It can only mean one thing, imaginary (or complex) numbers bridge that gap for us. And indeed, they do. Thus, they help us to appreciate mundane reality more broadly and to discern it more clearly. By way of imaginary numbers mathematical abstraction spills over into mundane reality. That not so simple “trick” of allowing an imaginary construct to enter our mathematics tool bag as described in the background section is what brought that broadening and clarity. As an example of this “spilling over” per the red font text, the overall opposition to AC current, i.e., the impedance of an AC circuit, which impedance is a real and tangible property of AC circuits, is comprised of a tangible (real) resistance (directly dissipates energy) and a conceptual (abstract) reactance (does not directly dissipate energy, but stores and exchanges energy between oscillatory electric and magnetic fields). Electrical resistance is quite tangible, reactance for its part is not, but it, notice, “bridges the gap,” by connecting actual physical behavior (real, tangible impedance) with abstract phase relationships impacting the reactance contribution to impedance. Phase has to do with the relationship between two or more waveforms, and waves per se, i.e., oscillations, are rather abstract in and of themselves, so no surprise here that reactance comes in on the conceptual | imaginary side of the impedance computation. Given Z is impedance, R is electrical resistance, and X is reactance, we have this real-world computation for Z:

 

Z=R + X i

 

Notice that Z follows the complex number format shown above (a+b i), Z here has (a=R, b=X), it follows that Z is a complex number, that is, a “grain” in the complex number plane (compare a previous example, Fig. 2). In that previous example we determined that the modulus was 4.47 and the angle of orientation was -26.6 degrees from the positive real axis, what would that mean in the context of impedance? It means that the impedance, the opposition to the flow of AC current, has a value of 4.47 ohms, which is high or low depending on the context of the circuit. For example, in RF (radio frequency) circuits, impedances are often standardized to 50 or 75 ohms, so 4.47 ohms would be considered very low. And moreover, the negative angle of 26.6 degrees that we calculated before means that the inpedance is influenced by a certain kind of reactance, capacitive reactance–there is one or more capacitors in the circuit or general capacitance bearing elements are present that comprise 2 ohms of capacitive reactance Xc, from which, according to the formula Xc=1/(w C), where w relates to the frequency of the AC circuit, the actual capacitance C may be determined. The resistance to reactance ratio can be read right off the complex impedance Z= 4-2i, in ohms we have 4 to 2 or 2 to 1, more pure resistance than capacitive reactance. In AC circuits, a negative angle means the current leads the voltage which is characteristic of capacitive reactance (“lead” means the current “through” the cap reaches its max/min slightly before voltage across the cap reaches its max/min). This “leading” (or lagging in other cases) is called a phase shift between these two waveforms. We get a phase shift because capacitors store energy in an electric field and release it back into the circuit when they discharge, causing the current to lead the voltage. Simply put, when the cap is fully charged, potential V (and Efield) across it are at their maximum, but the current “through” the cap is zero because it is fully charged and cannot take anymore charge on board–no charge is moving from the circuit “through” the cap therefore, which charge movement by definition is current, so voltage is max and current is min here, alternatively as the cap discharges, the current “through” it and into the circuit ramps up, but V across the cap decreases because it is giving up the charge that setup the potential V across it in the first place ( the cap is losing the energy stored in its Efield now), so voltage is min and current is max here. Clearly, it is the charge/discharge action, and thus ultimately current, that determines the voltage across the cap–current necessarily leads here. This lead/lag | max/min phenomenon tracks the sinusoid of the AC generator, it is a phenomenon altogether characteristic of the phase difference between the current and voltage in a cap. More generally, current through a cap is like so:

current= C dV/dt.

This says that, due to the energy storage and discharge process assumed to be going on, C, the ability of the cap to store charge (depends on its geometry and makeup), times the variation of the voltage it senses at its terminals, sets up the current “through” it. The cap’s terminals are assumed to be hooked up to a circuit driven by an AC generator that varies the voltage across the cap according to dV/dt. The voltage change dV/dt at the cap’s terminals causes the associated Efield across the cap to push and pull charge onto and off its plates causing charge to move, which is current by definition. So, it is the Efield that does the heavy lifting that establishes the current bottom line, even though we do not see “Efield” in the formula (recall that Efield, and force, and potential are mathematically related)–the Efield provides the “umph,” the force, that moves charge around which movement is current. The “C” term scales the current that could possibly come about because it is related to how much charge the cap can store and release in response to the Efield. Now, in a purely capacitive circuit, the phase shift is 90 degrees, in this example we can deduce from the Z= 4-2i impedance that the circuit is not purely capacitive–Z is not purely imaginary–and given the impedance angle of -26.6 degrees that we calculated before, it follows that the current leads the voltage by precisely 26.6 degrees (it quantifies the max/min “race” between current and voltage for this circuit).

 

It is a real thing this opposition to AC current Z, but the mathematics, the only mathematics in fact that captures Z and makes it “real” for us consists of an imaginary component (reactance). As can be seen from this example, a complex number “grain” in the complex plane packs a lot of information–one’s imagination (!) is the limit as to what can be gleaned from real-world problems when tcleverly ranslated onto this simple “geometry” we call the complex number plane.

 

Cartography, fractals, Fourier and Laplace transforms, waves, wave functions… imaginary numbers literally permeate our mathematical and scientific domains. They are let’s say “a useful fiction,” integral to our universe-language computation of relationships that we cannot “touch” but clearly “see.”

 

The Additive Identity Zero (0)

 

Background

 

The Additive Identity, Homogeneous Equations

 

Zero serves as the additive identity in mathematics. When added to (or subtracted from) any other number, it leaves that number unchanged. Its modern use can be traced back to Indian mathematics. Indian mathematicians (esp. Brahmagupta) developed a sophisticated numeral system that included zero. This numeral system was transmitted to Europe via medieval Islamic mathematicians (esp. Al-Kwarizmi), who played a crucial role in preserving and disseminating mathematical knowledge. Fibonacci, an Italian mathematician, popularized the use of zero in Europe during the Middle Ages. Interestingly, the Maya civilization independently used zero in their numerical system. The Maya understood zero as a placeholder, allowing them to represent larger numbers efficiently.

 

Let’s do a simple example that demonstrates the role of 0 as the additive identity. Let’s consider the equation:

 

gx+h=0, where g and h are constants, and x is the variable we want to find. The solution involves isolating x:

Subtract h from both sides to get:

gx+h-h = 0-h,

gx= -h+0 (0-h is identical to -h+0),

gx = -h by the additive identity (adding 0 to -h leaves it, i.e., -h, unchanged),

Now divide both sides by g to find x:

x=-h/g

 

Simple enough, maybe too simple, but without 0 in its role as the additive identity we would not have a starting point to balance the equation. There is something important and interesting about this simple example though. Equations that have a right-hand side (rhs) equal to 0 are called homogeneous equations, and solutions to homogeneous equations are general solutions, that means it includes all solutions that are natural to the underlying problem. The general solution accounts for all values of the variables that satisfy the equation, which encompasses both the trivial solution (where all variables are zero) and nontrivial solutions (where at least one variable has a nonzero value). However, in our example, since we only have one equation, we call this homogeneous solution the “particular” solution. If we were dealing with a more complicated scenario where we had a system of equations represented by some matrix, let’s call it A, and with rhs represented by b, then for the homogeneous linear equation Ax=0 we would call the solution to that system of homogeneous equations the general solution. We can go a step further, still focused on zero. The general solution to the Ax=0 system of equations has a solution x that is necessarily a vector (an n-tuple of directions), actually, this n-tuple is a vector space called the “null space.” When the matrix A comprising our system of equations operates on objects in its null space it gives the zero vector—all directions therein get collapsed to zero, i.e., to the origin. That means we have found our x for each equation such that the linear system Ax=0 is satisfied—it is precisely the null space of A. Now if we were to modify the rhs and make it nonzero, we get a nonhomogeneous equation, namely, Ax=b. It is the same system of equations A, but with rhs now equal to some nonzerio vector b, itself representative of external stimulus imposed on our underlying problem. That typically is the essence of the rhs in real-world problems—it is how the outside world enters the problem. It means we are looking for a solution that came about due to external influences on the underlying problem coming from the outside world, stimulus embodied in the rhs. We call this a particular solution as well even though it came from solving a system of nonhomogeneous equations this time rather than a single equation like in our simple example. Putting it all together and sticking with the system of equations context, the general solution (homogeneous solution) plus any appropriate particular solution (nonhomogeneous solution) gives the complete solution to a nonhomogeneous equation. Why does that matter? Because homogeneous equations tend to be simpler both conceptually and in the math-mechanics needed to solve the thing, while nonhomogeneous equations require additional steps to handle the nonzero rhs, which may be difficult for that given rhs, but if we can find another particular solution via an appropriate simpler rhs, then together with the typically simpler to find general solution, we have the complete solution to the difficult nonhomogeneous equation that posed problem solving difficulties. In short, if we find another but appropriate particular solution, then together with the general solution, we cover all possible rhs scenarios presented by that nonhomogeneous equation’s left-hand side (lhs). That is exceedingly powerful, indeed liberating, as far as solving real-world problems goes, problems that certainly present us with all manner of rhs, usually quite difficult to solve. The method of undetermined coefficients is one way to choose an appropriate rhs; it is a powerful technique for finding a particular solution to nonhomogeneous linear differential equations. It allows us to select an apt form for the particular solution based on the nonhomogeneous term, i.e., based on the rhs itself. It involves intelligently guessing a particular solution based on the form of the nonhomogeneous term. That is, we choose a function that matches the rhs but includes undetermined coefficients. Then we substitute that guessed particular solution into the original differential equation. Then by equating coefficients, we solve for the undetermined coefficients. This gives us the complete desired (appropriate) form of the particular solution. The works cited and references section below contains a link to an MIT video demonstrating the method with a more complicated differential lhs. The complete solution combines the homogeneous solution, i.e., natural behavior, with the particular solution, i.e., behavior owing to external stimulus. It accounts for both the problem’s natural, inherent effects (homogeneous) and the impact of external stimulus on the problem (nonhomogeneous).

 

A little more on particular solutions. In what follows, please note that in general equations are considered to be constraints, and variables are considered to be degrees of freedom (dof). Insofar as the role of constraints and dof, we have worked through a few examples that show how linear algebra finds its solutions that might be of interest. Figure 3 is the full rank case where we have as many equations (constraints) as unknown variables (dof), this presents us with exactly one particular solution, or possibly none. Figure 4 is the full column rank case, it is over-constrained, we have more equations (constraints) than variables (dof), this presents us with either exactly one particular solution or none. Figure 5 is the full row rank case, it is under-constrained, we have more variables (dof) than equations (constraints), this presents us with either exactly one particular solution or bunches coming out of the null space (see rank). Imagine trying to stretch a rubber band laying on a tabletop, in order to stretch it, one end must be held fast, i.e., constrained, if not, one cannot stretch the rubber band, it will only pull along, it will behave as it wishes, in response to a tug it maybe will loop in on itself, or maybe roll up and entangle, or flop around or whatever, the response to my pull is entirely inconsistent, there is no “solution” here, my rubber band will not stretch as I wish it too, there are responses indeed, many varied deformations as I pull, but not the one I wish—this is the under-constrained debacle of figure 5, if that rubber band were glued to the tabletop here and there, then maybe it would stretch when pulled on, but more than likely it wouldn’t budge, this is the over-constrained debacle of figure 4, if we hold fast one end then we can tug on the other end and stretch it no problem, it will respond consistently, it will manifest my intended stretch-solution, this is the sweet full rank problem of figure 3—exactly one particular solution—constraints and dof offset (yet there might be no solution, e.g., the equations may be linearly independent thus manifesting full rank, but describe parallel lines–no solution-intersection possible therefore: in the rubber band analogy, it is as though the rubber band is rigid along the length of its own fibers, no deformation or stretching is possible). Generally,  balancing constraints and dof ensures meaningful solutions. So, once again, the number zero shines, here in the context of real-world problem solving as concerns balancing equations, zero rhs, and null spaces.

 

Division by Zero

 

When some nonzero number is divided by a number less than 1 but greater than 0 the result gets larger and larger the closer the divisor gets to 0. Why is that? Imagine a couple of even-sized (vegetarian) pizzas laying side-by-side. Cut the one on the right into four even-sized slices. Grab a slice, let’s call it a template slice, and overlay the pizza on the left with it—it will perfectly cover four sections one after another of that other pizza. Now let’s divide down our template slice, let’s halve it. Grab a template and overlay the other pizza—It will perfectly cover eight sections one after another of that other pizza. Keep downsizing your template slice until you have a slice that is very small, let’s say the size of a crumb. Now overlay the other pizza with that crumb template one “crumb section” after another—it might take the rest of your life to do it. The point is that the smaller we make our template divisor, the larger the number of coverage sections we visit when overlaying the other pizza. Suppose we somehow cut down our template slice to the size of the diameter of the hydrogen atom, a tad more than an angstrom—wow, imagine how many coverage sections that template would need to visit to cover the entire pizza—for sure you would spend the rest of your life managing that. Since the template is so small, one needs an astronomically large number of (angstrom-sized) “crumbs” to cover the entirety of the other pizza. Mathematically, we say that the overlay coverage number “approaches infinity.” One never truly reaches infinity because smaller and smaller crumbs cannot cover the whole pizza—the crumb-template “divisor” downsizing approaches zero, but never reaches it. So, we see that dividing by a tiny number approaching zero makes the result larger and larger, eventually heading toward infinity (Fig. 6). But please note, when one actually divides any non-zero number by zero, the result is undefined. Why? When we say “a divided by b,” or, a/b, we are distributing b across a, we are diluting a by b. When we distribute seven apples amongst seven people we want to know how many apples per person, which is (7 apples)/(7 persons), or (1 apple)/person. But dividing seven by zero, or 7/0 in the apples per person context is like trying to distribute 7 apples among 0 people or (7 apples)/(0 persons)! Intuitively it’s an easy call, the distribution does not happen, but mathematically, there is no meaningful way to do it—this is an undefined mathematical result even though it is not entirely absurd logically—logically, one assumes the distribution simply does not happen. Practically, this undefined result does not have direct utility in most mathematical contexts. Some “exotic” number systems do allow division by “something similar to zero.” For example, in nonstandard analysis, hyperreal numbers introduce infinitesimal quantities that behave like tiny numbers close to zero. Still, these systems are more theoretical than practical. In projective geometry, we encounter different “infinities” associated with various directions in vector spaces. Each direction has its own “infinity,” but projective spaces do not fit the typical notion of a “number system.” So, while division by zero remains undefined in standard arithmetic, exploring alternative number systems and abstract concepts is the way of the future, who knows what discoveries chasing that rabbit down its rabbit hole might bring.

 

Zero over against Nothing

 

Zero is a number (0), it is an integer, in fact, it is a whole number (whole numbers are the set of counting numbers along with 0). In a strictly material sense, 0 can be utilized to develop a mathematical basis for “nothingness” in the context of set theory through the notion of “absence.” Consider the mathematical construct termed “empty set” (denoted by { }—a set of empty braces). An empty set contains no elements; it represents the absence of any objects. The cardinality of a set refers to the number of elements it contains. The empty set has a cardinality of 0 because it contains no elements. When we encounter situations where there is nothing (no quantity, no value, no objects), we often use 0 to represent that absence. If one has 0 apples, it means there are no apples—”apples nothingness.” The temperature of absolute zero (0 Kelvin) represents the absence of thermal energy to the extent that molecular motion ceases. The universe, i.e., the set of “everything” denoted {everything} sprang from absence, from the empty set { }, entirely without outside agency—does the reader, beyond your amusement, suspect that something is wrong with that picture? That is a well-disseminated, popular notion in Godless, secular academia. Note again what they teach, they say that {everything} sprang from { }, entirely without outside agency. If the empty set { } were singularly the origin of {everything}, it would imply that all elements, necessarily including the empty set itself (!), somehow emerged from guess what—a circular nothing—indeed their reasoning is circular at best, and flat-out absurdity at face value. We are not implying that {everything} is some mere universal set here, it is bigger and of course…it is real. But we must take care to conceptualize this “nothingness,” this absence, in a strictly material sense when utilizing a mathematical basis such as { }. Beyond mathematics, the concept of “nothingness” might consider philosophical questions about non-being, non-existence, and void, which we disallow in our mathematical conceptualization of “nothingness.” So, 0 serves as a practical way to express absence, whether in sets, measurements, or everyday contexts (the deeper philosophical notion of “nothingness” goes beyond mathematical formalism, so we are not interested in that here). Mathematically, zero and “nothing” intersect in absence.

 

Reality Intersection

 

Zero plays a crucial role in our reality across various areas of knowledge and disciplines. We have lightly touched on some of the mathematical roles. If we were to pinpoint the most profound intersection of zero with our mundane reality, it would be its role as a foundation for counting and measurement. Zero is the starting point for counting, it is the void from which all numbers emerge. While starting from one is much more intuitive for everyday counting, zero-based indexing and mathematical consistency drive the choice to begin with zero in certain contexts. Bottom line, without zero, our numerical system would lack a reference point for enumeration. Whether we are counting apples, days, or whatever, zero provides the baseline. It is the origin on various scales, for example, absolute zero (0 K) is the lowest possible temperature as said before, midnight (00:00) marks the beginning of a new day, the origin in 3D Cartesian coordinates is {x=0, y=0, z=0}, i.e., {0,0,0}. These scales allow us to measure and compare quantities and make computations therefrom. And of course zero represents “nothing,” that is, the absence of quantity. So in essence, zero is not simply a digit, it could be argued that it is sort of a “silent hero fiducial” upon which our mathematical, scientific, and practical mundane reality rests.

 

But quintessential reality is God’s reality, it is Truth—we find it in His Word. Every detail of that Word holds profound significance in that regard. While the number zero is not explicitly mentioned in that Word, in the Christian Bible, its symbolic meaning is deeply rooted in the Bible’s spiritual and theological concepts. For example, the Bible begins with the profound statement: “In the beginning, God created the heavens and the earth” (Genesis 1:1). Before creation, the earth is described as “formless and void, and darkness was over the surface of the deep” (Genesis 1:2). This primordial state represents the absence of form, matter, very existence—a vast expanse of nothingness awaiting God’s creative intervention. It is not hard to see zero associated with the void and serving as a metaphor for this state before creation. In this way it symbolizes pure potentiality, potentiality waiting to be transformed by our Creator God. So, in a way, through zero, it is just a short mental step to get a glimpse of God’s sovereignty over nothingness. His spoken Word brought forth light, shaping the universe from absence, from emptiness, and in that context zero betrays God’s eternal existence back yonder before space and time. In the biblical numerology zero could also signify brokenness, and emptiness, emptying self, and purity, and surrender, surrender to God’s will—a state of openness and reliance on our Creator God’s divine guidance. Is that not a better reality to intersect with personally (“A Letter of Invitation”?

 

The Multiplicative Identity One (1)

 

Background

 

The ancient Babylonians and Egyptians understood the concept of “unity” and used 1 as a fundamental building block in their mathematical systems, they laid the groundwork for the number’s later mathematical developments. Mesopotamian mathematics, particularly Sumerian mathematics, was integral to Babylonian scribal training, and geometry played a crucial role in that training insofar as dividing land plots for farming and irrigation. The development of early principles of geometry accrues to them (3000 BC); their geometry was practical and empirical, arising from needs in astronomy, construction, crafts, and surveying. While indeed advanced for its day, Mesopotamian mathematics was not as refined as Greek mathematics came to be. Thales of Miletus (around 585 BC) is considered the first Greek mathematician. He developed then known geometry and introduced practical applications thereof. Pythagoras, influenced by Thales, made mathematics central to his philosophy. His student Hippasus discovered irrational numbers. Philolaus developed the sun-centered (heliocentric | pyrocentric) model of the universe, and Archytas (a Pythagorean, but not to be confused with Pythagoras) taught Eudoxus, another brilliant mathematician and astronomer. These mathematicians influenced the works of Plato and Aristotle, whose philosophies were informed by mathematics, especially geometry. Bottom line, the concept of “1” as unity was recognized by the ancient Babylonians and Egyptians, but it was the Greeks who elevated mathematics to a deeper understanding of reality including the concept of “1” as unity.

 

If the reader has little or no background in mathematics, feel free to skip the following definition section without too much loss of generality, no problem. We have linked sort of esoteric math ideas and terms to explanatory sources to help clarify things.

 

Definition: In a set equipped with a binary operation called a product (denoted by .), the multiplicative identity is an element e such that,

 

e.x = x.e = x, for all x in the set.

 

Notice that x did not change when multiplied by e in either direction, i.e., under commutation—that is the multiplicative identity effect of e we are considering, and x can be any of the linked algebraic structures of the next couple of sentences (of course the identity matrix is e not x, so discretion please). The definition may seem like overkill on the one hand because it is so obvious and yet vague on the other because it is very general. Essentially, we have this: for a given multiplicand structure x we have a specific identity element e, such that under a product operation between e and x, x remains unchanged; e here stands for some “ identity element,” it is not the Euler’s number e which we discuss separately later. In the ring of integers Z and its extension rings (such as the field of rational numbers, the field of real numbers, and the field of complex numbers) e serves as the multiplicative identity, typically per the number one. For the set of matrices with entries in a unit ring, the identity matrix is the multiplicative identity e with respect to matrix multiplication (the product). In transformation groups (e.g., symmetric groups), the identity map on the set is the multiplicative identity, i.e., the identity map is e (given the set X we have an identity map denoted id_X, it satisfies id_X[x]=x for all x in X—the product is map composition, the identity element e is the identity map, which leaves every element unchanged as shown, and acts as a baseline or reference). If we consider Boolean operations as a product, the universal bound corresponds to the multiplicative identity e. Uuniversal bound  law: For any element a in a Boolean algebra, we have:
a + 1 = 1 (where 1 represents the universal bound) and.
a · 0 = 0 (where 0 represents the universal bound).

The first part states that any element combined with the universal bound (1 | True) results in the universal bound itself. In other words, it’s like saying “adding everything to infinity doesn’t change anything.” The second part indicates that any element combined with the universal bound (0 | False) results in zero. This reflects the idea that “multiplying by nothing gives nothing.”

Lastly an aside as per the number one—it is not universally considered a prime number, it represents the smallest possible difference between two distinct natural numbers.

 

Let’s step back in time a couple of millennia or more—would it have seemed intuitive to an ancient that e.x = x.e = x? Probably not. The notion that there exists a special element that, when multiplying another element (self or otherwise), leaves that other element unchanged (i.e., e·x = x·e = x) requires a certain level of mathematical abstraction. Ancient mathematics primarily dealt with concrete, specific quantities (measuring fields, counting goods, etc.) rather than abstract algebraic properties. Later mathematicians, especially Greek mathematicians such as Pythagoras, Euclid, and Archimedes, explored more abstract and theoretical aspects of mathematics. Pythagoras’ school emphasized numbers, geometry, and mystical beliefs. The Pythagoreans likely understood the concept of unity, but whether they explicitly formulated a multiplicative identity like “e” is unclear (the rigorous study of algebraic structures, including fields, emerged around the time of Euclid—300 BC, and Archimedes a smidge later; Euclid focused on geometry, Archimedes was a polymath: engineering, math, physics). The Greeks laid the groundwork for more abstract mathematical thinking, but it took centuries for those ideas to crystallize fully. So, while the concept of a multiplicative identity is fundamental in modern mathematics and assumed quite out of hand, its intuitive understanding, if at all, would have varied among ancient cultures based on their practical needs and mathematical interests. But who knows, there may well have been an ancient that thought about it and grasped it fully but was not able to disseminate their thoughts so that recorded history could prove it.

 

Reality Intersection

 

The multiplicative identity, 1, can be appreciated as a profound concept that intersects our mundane reality in several ways.

 

• It symbolizes identity and unity. It represents the idea that an entity is unique and whole in itself (e.g., God).
• The property of 1 to leave any number unchanged when multiplied can be seen as a metaphor for stability and consistency. It reinforces the fact that certain fundamental truths or principles remain constant, regardless of external changes (Exodus 3:14, Deuteronomy 6:4, Malachi 3:6, Hebrews 13:8, Revelation 22:13, et al.).
• The efficacious simplicity of the number bespeaks its elegance; elegance yet with profound impact on complex systems, an indicator that simple, fundamental truths or principles often undergird the complexity of our reality.
• Its pervasive, non-altering identity operation intertwined with all of mathematics highlights the interconnectedness of mathematical concepts per se and, by extension, the interconnectedness of all things in the universe, a universe that decidedly “speaks that language,” which serves as a heads-up that even the most basic elements play a crucial role in the larger structure of our mundane reality.

 

Indeed, it is a simple yet powerful concept that ensures consistency and accuracy across various fields and applications. Its presence in our daily lives, and math-driven scientific endeavors, highlights its fundamental importance. In that regard, let’s “do the math.”

 

• In everyday calculations, multiplying any number by 1 has the property that it leaves the number unchanged, pretty much the theme of this section. That property is essential for what? For maintaining consistency in mathematical operations. For example, if one has five apples and multiplies by 1, one still has five apples (multiplying five apples by 1 means adding the set of five apples to something once, whereas multiply five apples by 2 means adding the set twice to something to get ten apples, and so on). What is that something? It is one’s dreamy teammate zero. See how God’s rules cannot be altered? Five apples times 1 remains five apples forever. It’s just the way He demands it to be. If it weren’t so, then what happens to our reality? If a person breaks that rule out of defiance or whatever, then what? Well, if an airplane designer did it, then some planes would crash and burn for sure.
• In algebraic expressions and equations, the multiplicative identity helps simplify and solve problems. For example, when solving for a variable, multiplying or dividing by 1 ensures the value “stays anchored,” i.e., remains the same, preserving the equation’s integrity (we will demonstrate this a little later). It sets bounds for and indeed it stabilizes our reality (Job 38:10-11, Proverbs 8:29, Jeremiah 5:22).
• In geometric transformations, the multiplicative identity plays a role in scaling objects. Multiplying the dimensions of a shape by 1 keeps its size unchanged, which is crucial for maintaining proportions in design and modeling.
• In physics, the concept of multiplicative identity is used in various formulas and calculations. For example, when calculating forces, velocities, or other physical quantities, multiplying by 1 ensures the values remain accurate and consistent.
• In programming and algorithms, the multiplicative identity is used to initialize variables and maintain values during computations. It helps ensure that operations do not inadvertently alter data (ouch).
•  In financial calculations, the multiplicative identity is used to maintain the value of investments, interest rates, and other economic indicators. For example, multiplying an investment by 1 keeps its value unchanged, which is important for accurate and reliable financial modeling.

Here is a simple example that could apply to any of the bulleted items. Suppose we had the equation:

3x+5=11, we want to find x, so isolate x:

3x=11-5

now invoke the multiplicative identity–divide through by 3 which isolates x:

3x/3=6/3, x=2, where 3x/3 is essentially 1x i.e., 1 times x, which is x by the multiplicative identity. One just sort of takes this multiplicative identity invoking step for granted after a while, but there it is and necessarily so. The bulleted examples are obvious enough but beneath the surface necessarily lies this not so simple construct we call the multiplicative identity, 1. We very much need this number, this 1, serving in its abstract role/s, we expect it to be part of the universe-language LogoS given the overall logical consistency and law-abiding nature of our mundane reality that language describes and is inseparably part of.

Euler’s Number (e)

 

Background

 

The mathematical number ( e ) is called Euler’s number. It is named after the Swiss mathematician and devoted Christian brother Leonhard Euler (the son of a reformed pastor/preacher), who made significant contributions to its study. The number e is approximately equal to 2.71828 and is the base of the natural logarithm (compare 10, which is the base of the common logarithm). It shows up in many areas of mathematics, particularly in calculus, complex analysis, and number theory. It is especially important in the study of exponential growth and decay (Fig. 7), as well as in the formulation of the exponential function ( e^x ), which has unique properties such as being its own derivative. The history of Euler’s number involves contributions from several prominent mathematicians besides Euler.

 

• The history begins with another devoted Christian brother named John Napier, a Scottish mathematician, who introduced logarithms in the early 17th century. Although Napier’s logarithms were not directly related to e, his work laid the groundwork for the development of logarithmic concepts.
• The first significant step toward the discovery of e was made by yet another devoted Christian brother, Jacob Bernoulli, in 1683. While studying compound interest, Bernoulli was trying to determine how wealth would grow if interest were compounded more frequently than annually. He discovered that as the number of compounding intervals increased, the value approached a limit, which we now know as e.

 

Although Bernoulli discovered the constant, it was Euler who extensively studied and popularized it in the 18th century. Euler introduced the notation “e” and demonstrated its importance in various mathematical contexts, including the aforementioned calculus and complex analysis.

 

Please fasten your seat belt beloved reader and behold profound things. Euler’s number appears in Euler’s identity, which beautifully connects e with the Dream Team members: Euler’s identity is e^(i pi)+1=0. There’s the Dream Team in red font connected by way of e. It means this by way of Euler’s formula:

 

e^(i pi)+1=0,

Cos[pi]+i Sin[pi]+1=0,

-1+0+1=0, where -1 comes from the cosine term and lhs 0 comes from the sine term.

 

So, we have here the Dream Team connection, {i, 0, 1,e pi}—our Dream Team, grounded in Euler’s number and Euler’s identity and Euler’s formula—how profound is that as per this not so little number e? How profound is that given the extensive indeed expansive role of these fundamental constants in our Lord’s creative design and handiwork? He frequently utilized these five constants when He created. He had them in mind, they are as fixed in the created order as is His very fingerprint—it is hard to miss that fact, one must really want to miss it to in fact miss it. What we see around us would not be what it is without these constants, that is crystal clear because we cannot describe that reality without them. And to think that one number, e, rooted in Euler’s identity and Euler’s formula connects them all is very elegant, it is remarkable, and it betrays an underlying design—that is how the principle of design works after all—that which is designed springs from a blueprint, and there it is, part of the fundamental constants of this created universe, the Dream Team of numbers, springing forth from a deeper abstraction, Euler’s identity and Euler’s formula. The Dream Team constants that spring forth are precisely the ones that “stitch” the whole universe together just right for a stable reality. Namely, our Lord needed so much of this, and so much of that, then He mixed in so much of something else, and then He stirred the whole thing up according to this other thing, and so on—precise this and that things here, unchangeable this and that things here, elegant this and that things here. And in so doing, in large part through these numbers, He set bounds which can never be changed. And note how that He kept this profound discovery, this revelation, “in the family” if you will. Isn’t that interesting praised be Father God? (It is okay to unbuckle from your chair only when the dizzying effects of the profundity have subsided.)

 

Reality intersection

 

Euler’s number is deeply embedded in the fabric of mathematics and science, it is a cornerstone of practical and theoretical applications therein. But the reality intersection that we are interested in almost jumps off the page—it is surely its central role in connecting the non-physical fundamental constants of our universe. These constants “stitch” our universe together and we cannot describe our universe without them—e^(i pi)+1=0 speaks volumes, best just to let it speak and prayerfully listen to that reality intersection revelation and all the while praise our Creator God. We praise you Lord. Amen.

 

Archimedes’ Constant (pi)

 

Background

 

The Babylonians (c. 1900–1680 BC) approximated pi as 3.125 per their calculations of the area of a circle. The Egyptians, per the Rhind papyrus, approximated it as 3.1605. Archimedes (287–212 BC) is one of the first to rigorously approximate pi (rigor: axiomatic integrity, contradiction, detailed calculations, geometric proofs, logical structure). He used the method of inscribing and circumscribing polygons around a circle to show that pi lies between 3.1408 and 3.142912, an amazing result for that day. The Chinese mathematician Zu Chongzhi (429–501 AD), calculated pi to be approximately 355/113, which is accurate to seven decimal places—{Chongzhi vs pi today} is {3.141592920 vs 3.141592654 rounded up—see just below for 100 decimal places}.

The Greek letter π was first used to represent the number pi by the Welsh mathematician William Jones in 1706. It was later popularized by Leonhard Euler in 1737. Georges-Louis Leclerc, Comte de Buffon, devised a probability method to estimate pi, known as Buffon’s Needle which we will discuss in a moment. With the advent of computers, the value of pi has been calculated to literally trillions of digits. Here it is to 100 decimal places:

 

3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170680…

 

That non-repeating, non-terminating number is always precisely the same for any circle’s circumference divided by its diameter. Of course, one cannot say that conclusively because we do not know how this number behaves near to or at its end (as an irrational number it cannot be expressed as a ratio of two integers, hence it continues forever without repetition in any of its decimal places, Euler’s number e behaves similarly) but for all practical purposes so far, the claim is valid. That seems rather remarkable and non-coincidental. As said before, we cannot describe the mundane reality around us without including the Dream Team in our description somewhere, these numbers “stitch” our universe together just right, and pi provides a certain kind of stitch here and there and everywhere. So, by definition, pi is the ratio of the circumference C of any circle to its diameter D: pi=C/D. The diameter of any circle is twice the radius R of the given circle, thus pi=C/(2 R), and it follows that C=2 pi R, and circling back around we have our definition—pi=(2 pi R)/(2R). (We put 2R in red font to highlight the role of the multiplicative identity in isolating pi–can the reader see how it works? (2 pi R)/(2R)=1 times pi= pi by the multiplicative identity–1 times anything leaves that “anything” unchanged.)

 

Suppose we had a circle of radius 1u, where u could be any unit. We want to inscribe this circle inside a square. Since the circle is inscribed, it touches the square at exactly four points, the midpoints of the square’s sides as shown (Fig. 8). What must be the side lengths of the square to do this?

 

Since the diameter of the circle is 2u, a given side length of the square must be 2u.

 

What is the ratio of the area of the circle to that of the square given that the area of the circle is pi radius^2 or pi (1u)^2 and that of the square is (side length)^2 or (2u)^2?

 

We have (pi (1u)^2)/(2u)^2 =(pi u^2)/(4u^2), the u^2 cancel and we are left with pi/4 (by invoking the multiplicative identity), which is roughly 0.7854. Why are there no units in the final answer? They necessarily cancelled; a ratio of similar things cancels the units by default. So, we are left with a bare number, pi/4, as the area ratio—it means that given any circle of arbitrary radius u, the circle-inscribed-in-square areas ratio will always be precisely pi/4. No matter the size of the circle, as long as it is inscribed in a square, the ratio of their areas will always be precisely pi/4. That is an interesting result. It highlights how much of the square’s area is occupied by the circle, the circle occupies approximately 78.54% of the square’s area, which is pi/4 times 100%. This constant areas ratio is a beautiful example of how mathematical relationships can reveal underlying patterns and symmetries in nature. It can be seen as a testament to the consistency and elegance of mathematical principles that govern the Creator’s handiwork. Not surprisingly, this ratio also appears elsewhere, for example in probability theory, specifically in Buffon’s Needle problem mentioned above. That problem involves dropping a needle of a certain length onto a floor with equally spaced parallel lines and calculating the probability that the needle will cross one of the lines. The solution to this problem involves pi, and the ratio pi/4 can be derived in certain formulations of the problem. In numerical methods, particularly Monte Carlo methods, the ratio pi/4 is used to estimate the value of pi itself. By randomly generating points within a square and counting how many fall inside an inscribed circle, one can approximate pi based on the ratio of points inside the circle to the total number of points. And practically, this ratio helps in understanding the efficiency of space usage, which can be useful in various settings, not least design and packing problems.

 

Reality Intersection

 

Whenever one measures anything circular, like a pizza or a clock face, one is indirectly using pi. Even the calculation of the volume of a cylindrical can of soda involves pi: volume_cylinder = pi r^2 h, where r is the radius of the can and h is its height—notice that pi r^2 is the area of a circle. Pi’s ubiquity in both theoretical and practical applications highlights its profound connection to the world around us. It is essential in calculating the circumference and area of circles, which is fundamental in designing anything circular, from wheels to domes and arches in architecture. Engineers use it to design and analyze structures involving curves, such as bridges, chassis, and tunnels. Pi is used in algorithms for wave-intensive signal processing, which is crucial for technologies like GPS, and MRI machines, and in compression algorithms for images and audio files. As concerns us here, it also appears in the natural world, such as in the shapes of rivers and the growth patterns of plants. For example, the arrangement of seeds in a sunflower follows a pattern that involves pi. It is a spiral pattern that maximizes seed packing efficiency[1].

 

And of course pi is integral to the equations that describe waves, such as sound and light waves, and in the calculation of orbits, and indeed the structure of the universe.

 

Concluding Comments

 

In this study we wanted to look at the non-physical fundamental constants of our universe, numbers that form the bedrock of our mathematical understanding, numbers that form the foundational basis for the mathematical structures describing physical laws. We referred to them as “the Dream Team” {i, 0, 1, e, pi}. Not a stretch here, these constants are dreamy for sure. They are every bit as important as the physical constants are when it comes to understanding the makeup and origin of our universe; the two sets were designed to work together and were implemented accordingly by the Creator. On the physical side, those constants provide the numerical values that make the abstract physical laws applicable to our mundane reality, but the non-physical constants are integral to that, because they provide the foundational basis for the mathematical structures that precisely describe those physical laws.

 

Why is the charge q on the electron ~= 1.602176634 x 10^-19 coulombs? It is a measured quantity, but why this value? No one knows why it is that value. We know what q is, we know why it should be the value that it is— so that it “shakes hands” aright with things downline, like the fine structure constant for example with which it is intimately related—but we do not know why this particular value of q suits the physics downline, we need a deeper and bigger picture, a Dove’s-eye view. String theory (theory of “everything”, quantum gravity) tried to explain it, but string theory, while providing insights into geometric algebra and black hole physics faces significant challenges and skepticism for lack of experimental evidence forged by its sheer complexity, Occam’s Razor?! For example, it posits 10^500 universes, so which one is ours? Consider this chain of cause and effect with regard to q:

 

nucleus–> atom–> molecule.

 

Charge q must be exactly what it is to maintain stable nuclei because such depend on a balance between the electromagnetic (EM) force and the strong nuclear (strong) force. But the strength of the EM force is characterized by the fine structure constant which in turn is characterized by q, q^2 in fact; the EM force causes all the protons (charge +q) in the nucleus to repel one another, and this action must be balanced by the strong force which holds protons and neutrons together. With that in mind, consider atomic structure, a slight shift in q’s value would shift the strength of EM forces within atoms, that is, between protons and protons in the nucleus, skewing that effect, and between protons and electrons overall in the atom, skewing that effect, such that atoms could not form in the first place. And then at the molecular level, if one supposes one could get there in the first place with a shifted q value, it would alter “normal” interactions between atoms, thus affecting chemical reactions, in turn greatly disrupting molecular formation and hence the possibility for life. For life to exist as we know it q must be exactly as shown. But why that specific value, and why the other fundament physical constants values, why are they specifically those values? Who decided that q would be that value and gate the EM force accordingly by way of the fine structure constant, and everybody else on down the pipeline would respond just right, and who set up the strong force exactly right to counterbalance the EM force affected by q—who decided to do that, you know, this is a thinking man’s game here, to suppose otherwise is nuts. So much for the physical side.

 

Let’s go to the other set, the non-physical constants, our pals the Dream Team {i=(-1)^1/2, 0, 1, e=2.1828…, pi=3.1415…) which is what this study was all about. Right away we see that things do not get any simpler—who decided on these values? These constants are the “glue,” the “stitches” as we have been referring to their effect, these constants stitch the universe together by providing the foundational basis for the mathematical structures describing physical laws. If it be possible, this latter set is more intriguing than the former, because this latter set is entirely abstract, whereas the former can at least be tied to some physical stuff if you will—charge on the electron (q), fine structure constant alpha (~1/137), mass of the less massive up quark (2.2 Mev/c^2), speed of an electromagnetic wave (c in a vacuum), etc. These constants are sort of “hands on” things if you will, precisely measured things. But compare i = (-1)^1/2—huh? Why is that in the universal recipe? Why can’t we do, for example, quantum mechanics without i? The mathematical structure of quantum mechanics would be fundamentally altered, making it challenging, if not impossible, to describe and predict quantum phenomena accurately if we did not use i. The use of complex numbers, including i, provides the necessary tools to capture the full range of behaviors observed in quantum systems—and quantum mechanics flat-out works, but ya’ gotta’ stick i in there here and there. A thinking somebody with some serious power to boot modeled it like that a priori. Are we suggesting that God used i? It seems like it, at least for the joy i must have given Him when He did His work for this realm we call our mundane reality. And then there is zero (0)! What a concept. Adding something to 0, multiplying by 0, dividing by 0, and all the rules that go with that to make sense out of our mundane reality by way of physical laws grounded in reality by way of physical constants that respond in a certain way to a 0 operation (stimulus). That is what we mean by a “stitch.” We talked about one (1). That is the multiplicative identity—we cannot describe our mundane reality without that stitch. And Euler’s number e, the growth and decay stitch, same thing, it is so fundamental to our mathematical picture of reality that the physical laws that describe that reality look silly without e’s place in them. Imagine stripping all our known mathematics of e! And pi, no pi, no way to appreciate curves, oscillatory behavior, geometry, trigonometry, quantum mechanics, Einstein’s field equations, and on it goes. The imaginary unit i does its thing and stitches, so too 0 stitches, 1 stitches, e stitches, pi stitches. This here Dream Team is just as finely tuned—by the thinking, powerful Creator God—as the physical constants are, otherwise, the seams would not be stitched up right in the language we have been using, let alone that they would be able to hold things together—no stable mundane reality—but in fact it is just the opposite, we do enjoy a stable mundane reality. How about a non-repeating, non-terminating practical number pi as an example of something finely tuned? Let’s say trillions of digits thereof, well, so far—we don’t even know how or where the rascal ends. Pi is not an artifact by the way; it is an abstract if you will. It fits the LogoS, the Language of, and inherent in, the cosmos.

 

Of the Dream Team members, {i, 0, 1} are infinitely tuned–they are exact numbers, otherwise they could not serve their various roles, identity for example. God made {i, 0, 1} to be exact numbers. (As concerns the uncertainty principle, the “exactness” of these numbers does not violate the that principle, because the contexts are different. The uncertainty principle involves the measurement of conjugate variables, e.g., position & momentum, energy & time, with inherent fluctuations per the measurement—that is what gave rise to the principle in the first place—so the contexts are completely different here.) The identities (Euler’s involving all, additive involving 0, multiplicative involving 1) are LogoS, the associated exact numbers make it real. The Designer provided both the logic and the numbers, of course—that realization should be enough to appreciate His hand in it, but there is more, there is the Dream Team set {e, pi}. These numbers are quite different, they are both irrational and therefore inexact, yet finely tuned in the extreme, they are non-terminating after all. But why the distinction? If e and pi were exact numbers, it would profoundly alter the fabric of mathematics and the universe itself, at least our understanding of this universe we call home. Pi is mathematically derivable and represents the ratio of a circle’s circumference to its diameter as said above. If pi were exact, mathematicians and physicists would suspect that something is terribly wrong with the universe, because it is inexact pi that shows up in countless calculations across various fields: electromagnetism (e.g., energy density of EM field), quantum mechanics (e.g, reduced Planck’s constant, rhs of uncertainty principle), relativity (e.g., in GR pi acts as a “calibration constant” to ensure that GR matches the Newtonian gravity inverse square law in the non-relativistic limit—weak gravitational field, velocity <<c), and other fields besides these. Nailing down pi exactly, if that were possible (certainly not), would lead to mathematical contradictions and paradoxes. If pi were exactly 3 say, circles would behave differently! However, the geometry of spacetime would probably remain unchanged, because that is governed by mass and energy distributions, which are independent of the value of pi, even though equatorial great circles of mass-energy sources like planets and stars would be altered; the universe’s mass-energy content, distribution of the same, remains unaltered because that is independent of pi. And if e were exact, it would impact complex numbers, Fourier analysis, and of course the values we compute in quantum mechanics (QM). In QM, energy eigenstates correspond to specific energy eigenvalues, and e appears in the exponentials that describe the time progression of these states, so if e were exact, the energy eigenvalues would change accordingly. The exponential operator involving e is used to progress quantum states in time, an exact e would alter the dynamics governed by this operator. And wavefunctions, which describe quantum particles, involve complex exponentials, they too would be affected. The normalization condition for wavefunctions relies on the integral of the absolute value squared of the wavefunction which includes e, an exact e would affect the normalization and probability distributions. Bottom line, QM calculations involve intricate numerical computations, if e were exact, it would impact the precision and accuracy of these calculations, we would have to recalibrate our models to account for the exact e. Probably the fundamental principles of QM would remain intact, but the specific numerical results and predictions afforded by an inexact e as we know it would greatly differ if e were exact. This number e describes growth (and decay), and growth is gradual, it is not jerky and abrupt–the Creator did not want exact here, He wanted inexact, and in that dress the growth can be incrementally smooth growth, and not something abrupt and maybe wild that snaps to some value every time the growth reaches a certain period. The need for e in exponential growth models is fundamental and arises from the natural behavior of continuous processes; e is the base rate of growth shared by all continually growing processes. It allows us to model compound, continuous growth, where changes occur at every instant (even faster than a second). Unlike simple growth rates where changes happen more discretely, e captures the essence of continuous change. For example, if e were exact, say 3, it would lead to abruptness, to jumps at specific intervals, in this case a tripling every unit of time. Base 3 lacks the smoothness of continuous growth we get with base e (notice how base 3 “swamps” base e Fig. 10). And the Creator made these two inexact numbers non-terminating—e for example can handle a lot of growth without introducing a crazy, step-like spike or reflection at some terminus, a terminus would introduce literal chaos when e stitches. And of course e is non-repeating, which ensures continuous, smooth growth. So, pi and e being exact would reshape mathematics, science, and our understanding of mundane reality in profound ways. The Creator did not have that sort of a mundane reality in mind when He created, that is obvious from what we see around us. By the Creator’s obvious foreknowledge of the eventualities, He made these numbers inexact, and their inexactness keeps our mundane reality lucid and stable, we mean lucid and stable with respect to our human experience and perspective and studies. On the other hand, the exact numbers must be so to serve their roles in the various identities we discussed, and there they are, just as intended. But the created order is not simply an identities-idealization, it is decidedly also a manifest computation (a stitching), and the set {e, pi} serves in that role perfectly.

 

When we compute say with e, we must, clearly, approximate it—but is that not like introducing an artificial terminus? Yes indeed it is. What we do is try to strike a balance between precision and practicality by approximating e and pi using algorithms, and defining tolerances. That is what we humans do, but that is not what the Creator did when He conceived of these numbers in their entirety and utilized them to stitch up His Creation. All along He had in mind to make them manifestly available to us through the LogoS, because we would need them to subdue and rule over His Creation per His charge, a Creation steeped in the Dream Team and thus describable and understandable by way of it. The set {e,pi} holds a very practical place in the Dream Team, and necessarily consists of inexact numbers; the logic behind that inexactness jumps off the page and it too shouts “design.” A thinking Somebody quite intelligent and powerful most assuredly thought this design through and then by way of their surpassing power put it all together and put it into place just right for His Glory and…for us to enjoy, subdue, and rule over—imagine that.

So, there are two sets of fundamental constants in the created order, physical and non-physical, there is an interplay between them, an interplay that finely tunes for life. The Creator’s handiwork is much more complex and detailed and interrelated than humankind has appreciated so far and probably ever will until it is fully revealed by our Lord, and until then, the best mathematicians and scientists from yesteryear and today and going forward delight to stand on the shoulders of that Giant, by His grace, thus allowed to clearly “see” various chunks of that elegant and excellent and extraordinary handiwork of His—also, and very much so, by His grace comes this clarity.

 

Praised be your Name great Creator God, even Agent of Creation, yea Jesus, whom we love and adore (John 1:1-3, Colossians 1:16). Amen.

 

Illustrations and Tables

 

Figure 1. A Granular Complex Plane. {0,0} at Black “Grain”.

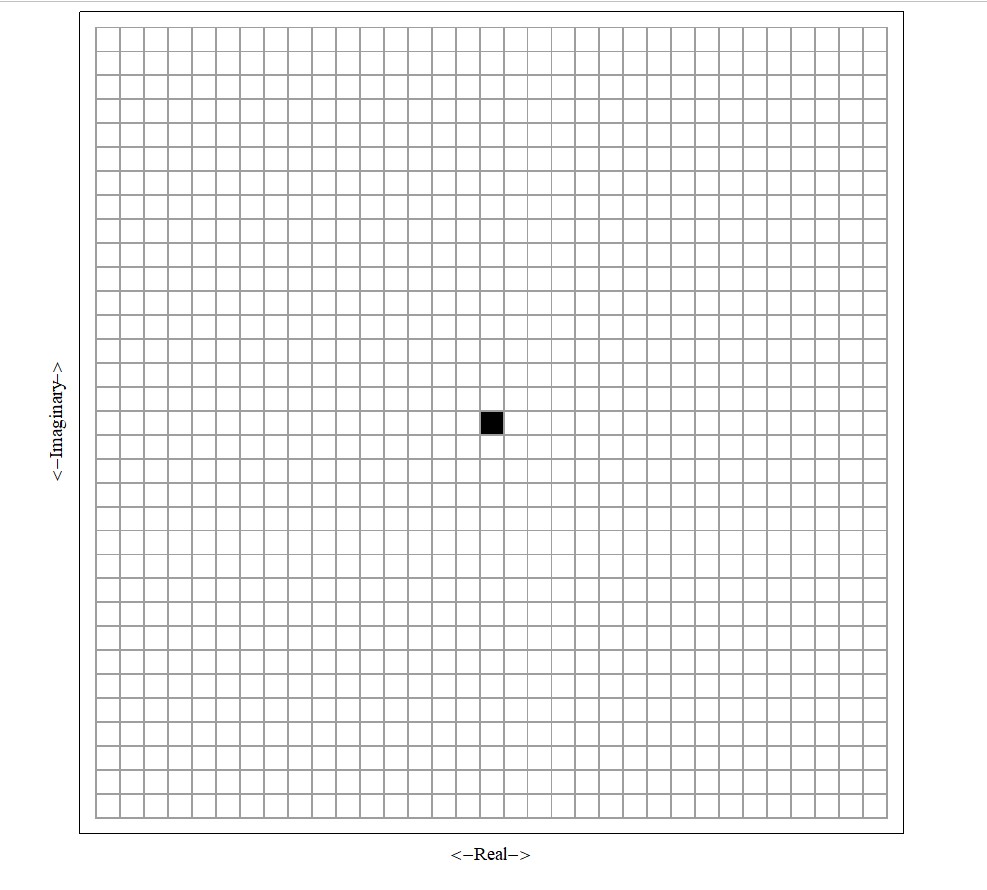
Figure 2. The Red “Grain” 4-2i or {a=4,b=-2} in the complex plane. {0,0} at Black “Grain”.

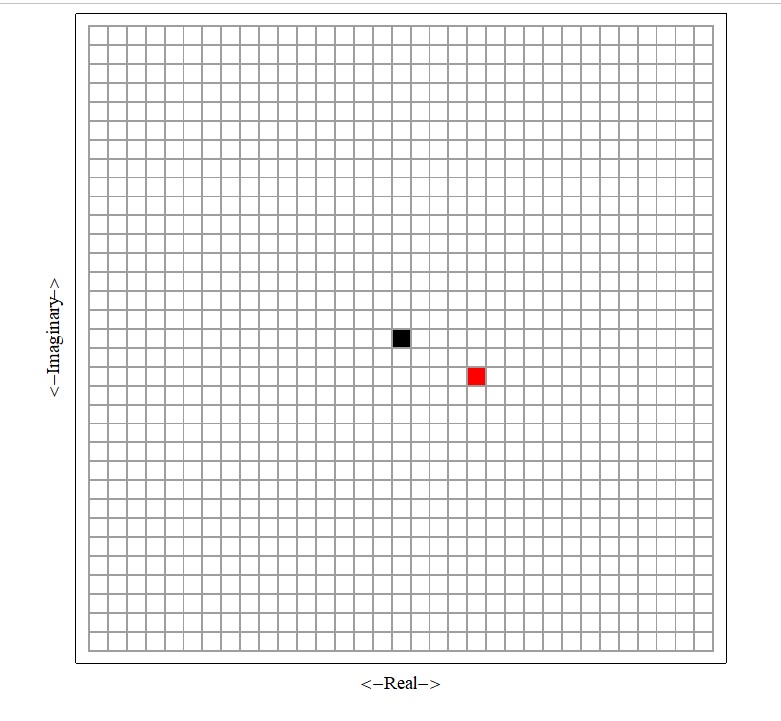
Figure 3. DOF Offset Constraints—Full Rank.

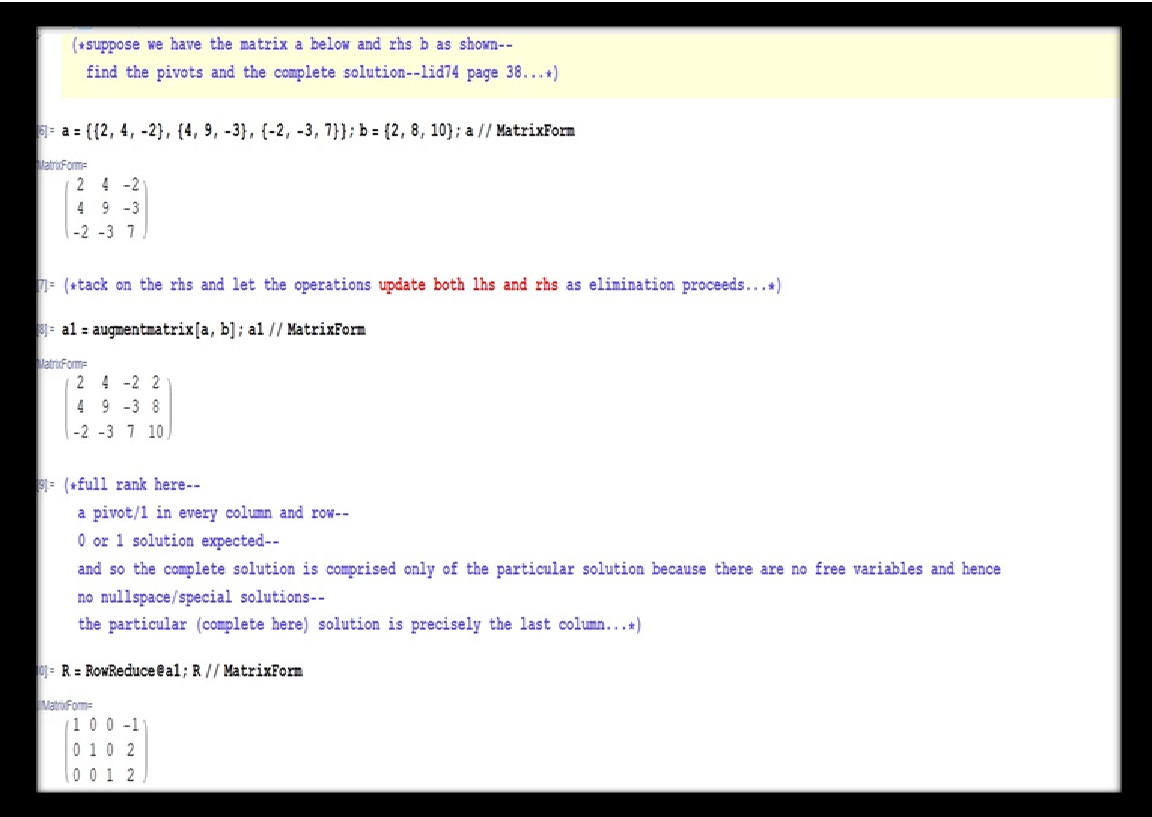
Figure 4. Dof < Constraints—Full Column Rank, Over-constrained.

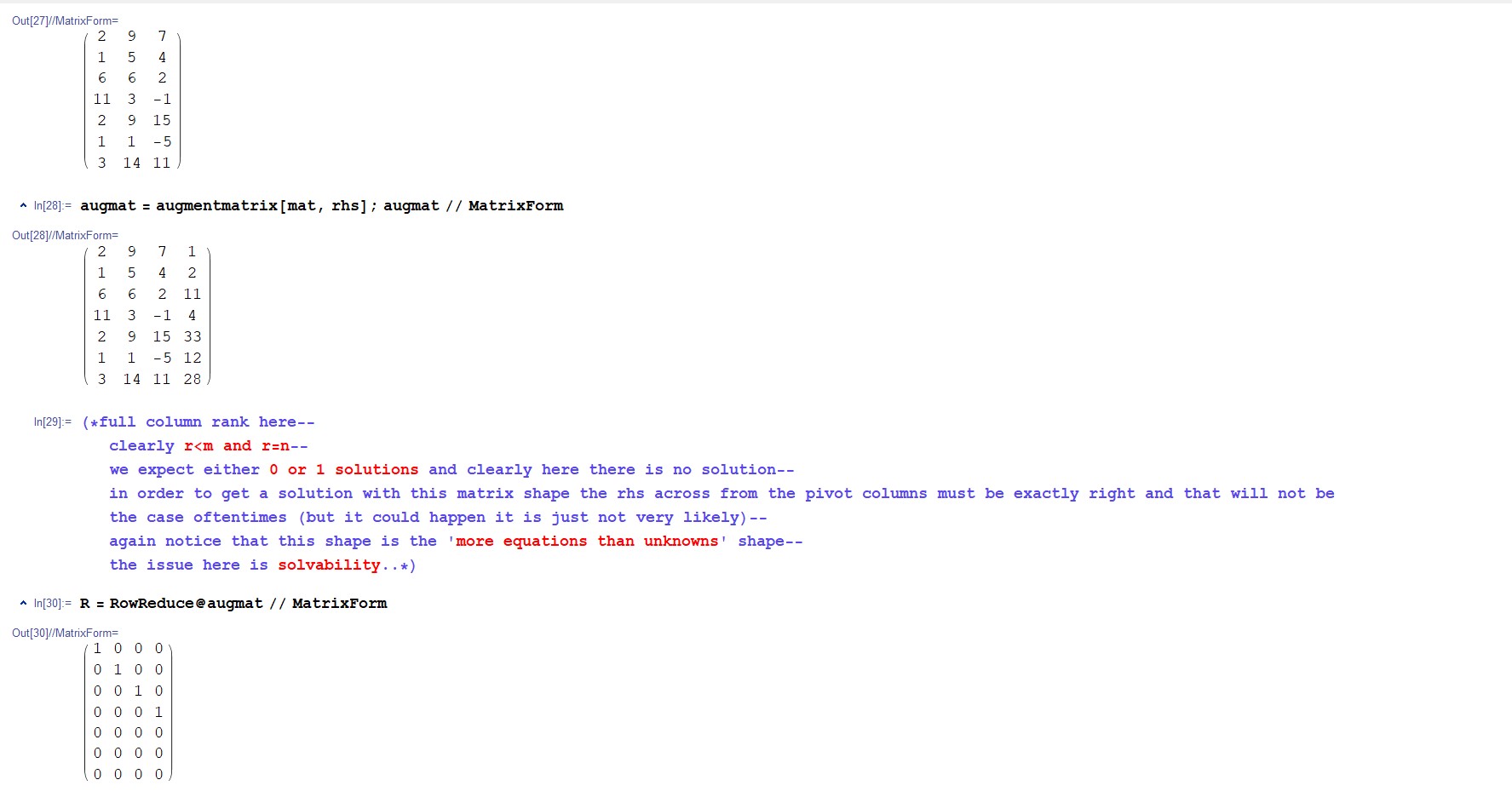
Figure 5. DOF > Constraints—Full Row Rank, Under-constrained.

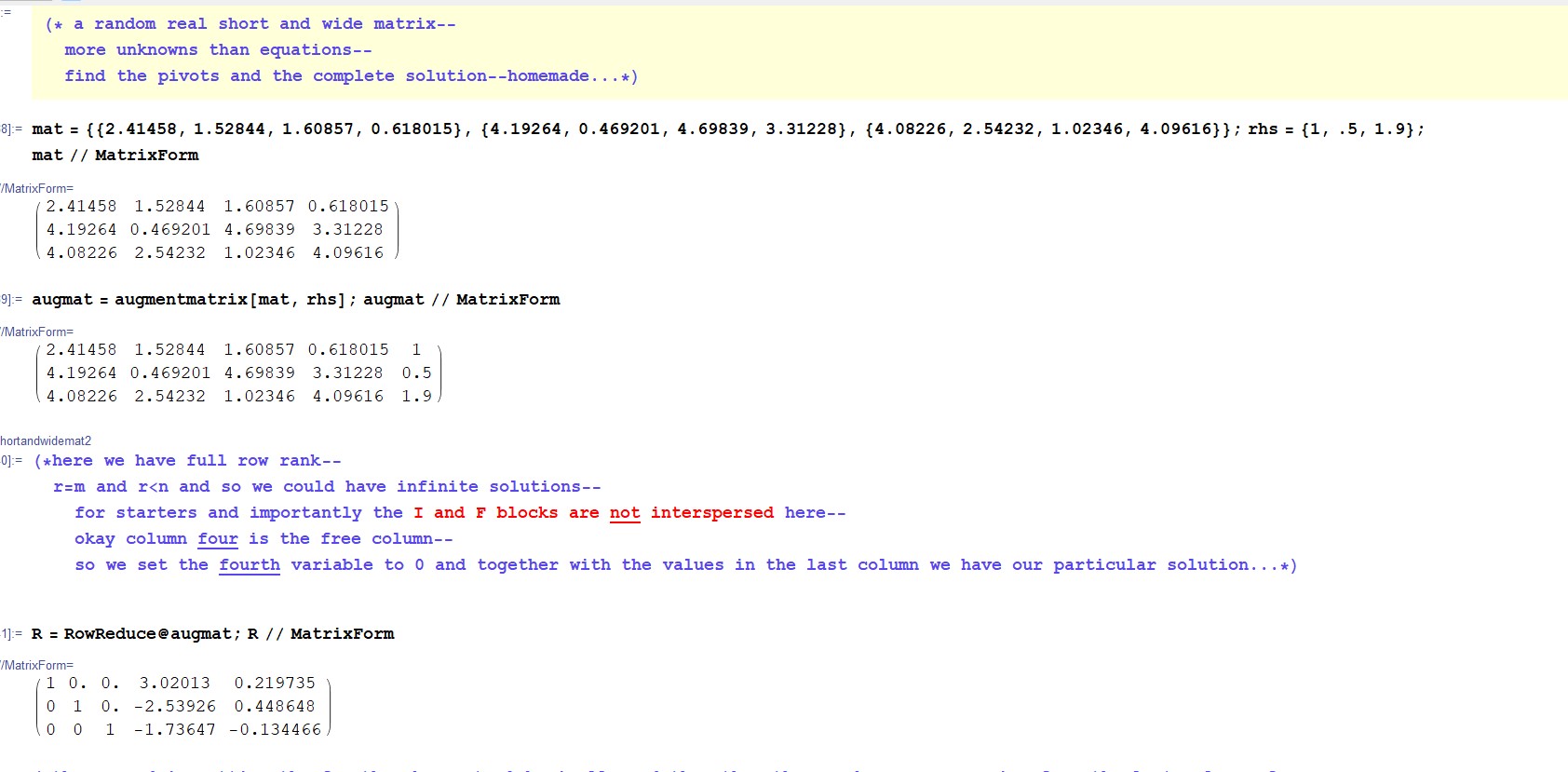
Figure 6. Division By Zero.

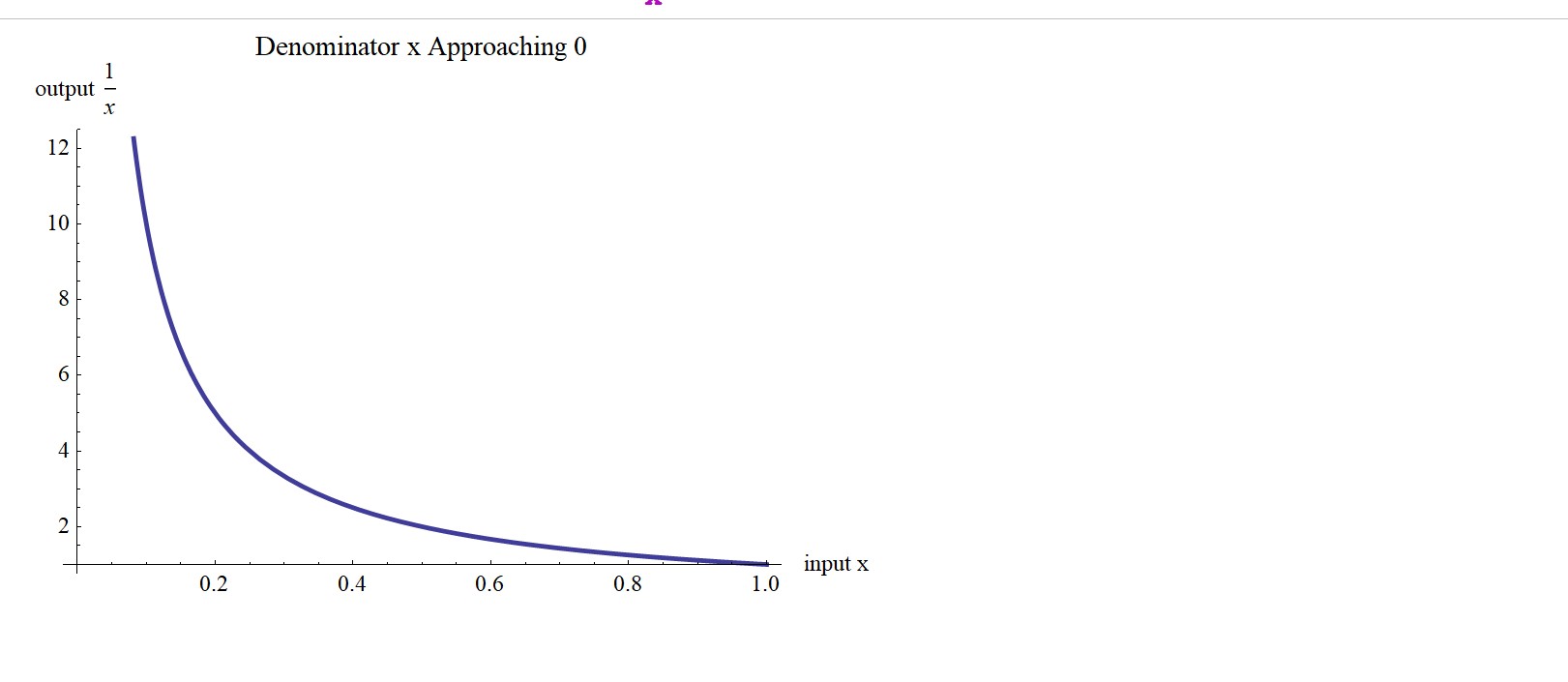
Figure 7. Delta [T] proportional to T at each instant -> exponential Decay | Growth.

Figure 8. Circle radius 1U Inscribed in Square.

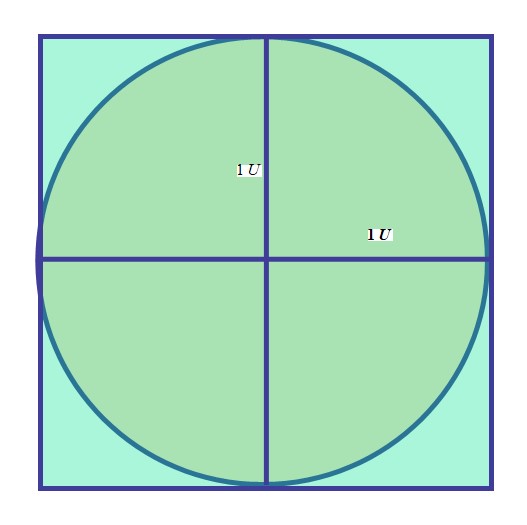
Figure 9. Golden Angle (dashed yellow-gray interface, ccw from bottom right where dashing starts) .

Figure 10. Exponential Growth Comparison.

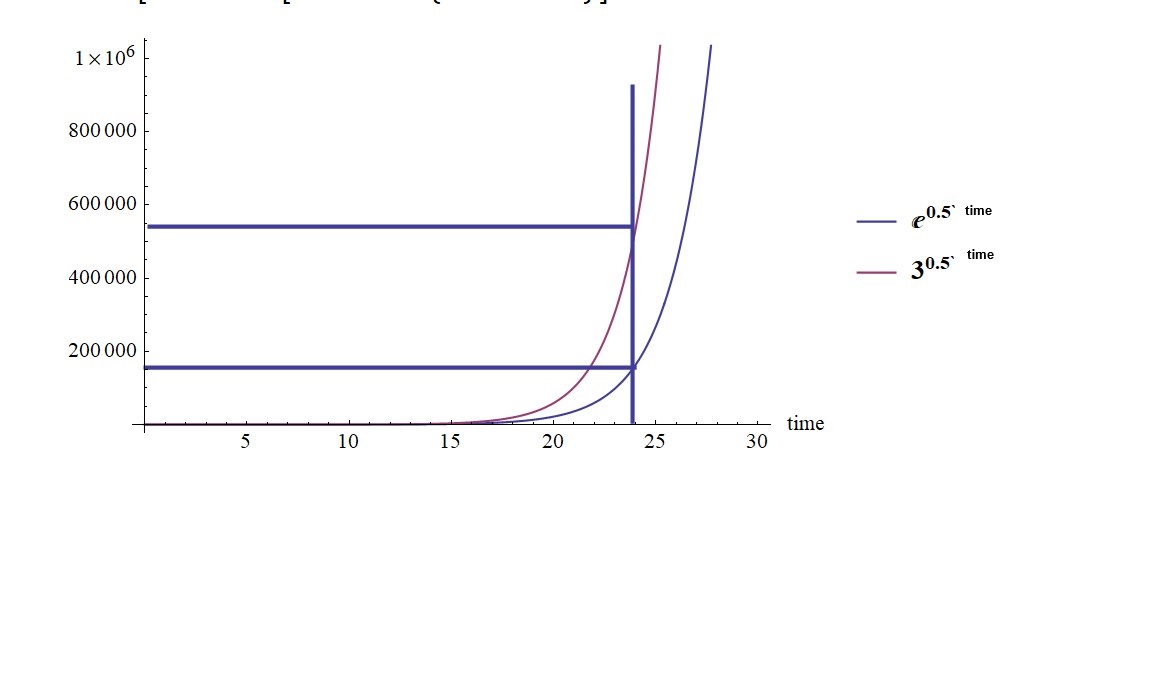
Works Cited and References

 

“A Letter of Invitation.”

Jesus, Amen.

< https://development.jesusamen.org/a-letter-of-invitation-2/ >

“Babylonian Mathematics: An Overview of Babylonian Mathematics.”

MacTutor.

< https://mathshistory.st-andrews.ac.uk/HistTopics/Babylonian_mathematics/ >

“Babylonian Mathematics: The Development of Mathematics Practices in the Mesopotamian Scribal Schools.”

SpringerLink.

< https://link.springer.com/chapter/10.1007/978-3-319-02396-0_5 >

“Algebra: Islamic Contributions.”

Britannica.

< https://www.britannica.com/science/algebra/Islamic-contributions >

“ Egyptian Mathematics: Ancient Egyptian Mathematics.”

Wikipedia.

< https://en.wikipedia.org/wiki/Ancient_Egyptian_mathematics >

“Egyptian Mathematics: “Mathematics in Ancient Egypt.”

Britannica.com.

< https://www.britannica.com/science/mathematics/Mathematics-in-ancient-Egypt >

“Euler’s Number: Discovery of the Number e.”

Brilliant.org.

< https://brilliant.org/wiki/the-discovery-of-the-number-e/ >

“Euler’s Number: How Does e Apply to Applications/Implications in Real Life?

Socratic.org.

< https://socratic.org/questions/how-does-e-2-718-help-apply-to-applications-implications-in-real-life >

“Euler’s Number: e (mathematical constant).

Wikipedia.

< https://en.wikipedia.org/wiki/E_%28mathematical_constant%29 >

“Euler’s Number.

MathMonks.

< https://mathmonks.com/eulers-number >

“Euler’s Number: Euler’s Number.”

UTSA.edu.

< https://mathresearch.utsa.edu/wiki/index.php?title=Euler%27s_Number >

“Euler’s Number: Euler’s Formula-a Complete Guide.”

MathVault.

< https://mathvault.ca/euler-formula/ >

“Euler’s Number: An Intuitive Undrstanding of Euler’s Formula.”

BetterExplained.

< https://betterexplained.com/articles/intuitive-understanding-of-eulers-formula/ >

“Euler’s Number: Euler’s Identity.”

Wikipedia.

< https://en.wikipedia.org/wiki/Euler%27s_identity >

“Euler’s Number: Euler’s Identity.”

SimpleWikipedia.

< https://simple.wikipedia.org/wiki/Euler%27s_identity >

“Euler’s Number: Euler’s Identity, the Most Beautiful Equation.”

LiveScience.

< https://www.livescience.com/51399-eulers-identity.html >

“Euler’s Number: Euler’s Number e Explained, How it is Used in Finance.”

Investopedia.

< https://www.investopedia.com/terms/e/eulers-constant.asp >

“Euler’s Number: Euler’s Number for Complex Numbers.”

MathisFun.

< https://www.mathsisfun.com/algebra/eulers-formula.html >

“Euler’s Number: Intuitive Understanding of Euler’s Formula.”

BetterExplained.

< https://betterexplained.com/articles/intuitive-understanding-of-eulers-formula/ >

Feynman, Richard.

Feynman Lectures on Physics: Algebra.

< https://www.feynmanlectures.caltech.edu/I_22.html >

“Geometry: History of Geometry.

Wikipedia.

< https://en.wikipedia.org/wiki/History_of_geometry >

“Imaginary Numbers.”

Science Notes.

< https://sciencenotes.org/imaginary-numbers/ >

“Imaginary Numbers: Geometrical Interpretation, Complex Number.”

Collegdunia.

< https://collegedunia.com/exams/imaginary-numbers-geometrical-interpretation-complex-number-mathematics-articleid-3782 >

“Imaginary Numbers: Intuitive Guide to Imaginary Numbers.”

BetterExplained.

< https://betterexplained.com/articles/a-visual-intuitive-guide-to-imaginary-numbers/ >

“Imaginary Numbers: Who First Came Up with the Idea of Imaginary Numbers.”

Papertrell.com

< https://www.papertrell.com/apps/preview/The-Handy-Math-Answer-Book/Handy%20Answer%20book/Who-first-came-up-with-the-idea-of-imaginary-numbers/001137022/content/SC/52caff7082fad14abfa5c2e0_Default.html >

“India: A Number’s Journey: Uncovering Who Invented Zero.”

HistoryCooperative.

< https://historycooperative.org/who-invented-zero/ >

“India: India’s Impressive Concept about Nothing-How India Gave us the Zero.”

BBC.

< https://www.bbc.com/travel/article/20180807-how-india-gave-us-the-zero >

“India: The Remarkable Story of Ancient India’s Gift to Mathematics and its Global Impact.”

Culture and Heritage.

< https://cultureandheritage.org/2023/05/zero-the-remarkable-story-of-ancient-indias-gift-to-mathematics-and-its-global-impact.html >

India: “What is the Ancient India’s Contribution to Mathematics.”

HistoryRise.

< https://historyrise.com/the-ancient-indian-contribution-to-mathematics/ >

“India: Unraveling the Enigma: Who Discovered Zero?”

Sakalnie.in

< https://www.sakalnie.in/blog/who-discovered-zero/ >

“Mathematics: Mathematics.”

Encyclopedia of Mathematics.

< https://encyclopediaofmath.org/wiki/Mathematics >

“Mathematics: The History of Mathematics.”

Wikipedia.

< https://en.wikipedia.org/wiki/History_of_mathematics >

“Mathematics: Why does Mathematics Interpret Reality?”

MindMatters.

< https://mindmatters.ai/2020/02/why-does-mathematics-interpret-reality/ >

Microsoft Copilot.

June 2024.

“Multiplicative Identity: Multiplicative Identity.

Wolfram Mathworld.

< https://mathworld.wolfram.com/MultiplicativeIdentity.html >

“Multiplicative Identity: Real Multiplication Identity is One.”

ProofWiki.

< https://proofwiki.org/wiki/Real_Multiplication_Identity_is_One >

“Numerical Analysis.”

Wikipedia.

< https://en.wikipedia.org/wiki/Numerical_analysis >

“Numerical Analysis, Introduction.”

UCSB.edu.

< https://web.math.ucsb.edu/~hdc/public/Introduction_Numerical_Analysis.pdf >

“One (1).”

Wikipedia.

< https://en.wikipedia.org/wiki/1 >

“Pi: Pi.”

Wikipedia.

< https://en.wikipedia.org/wiki/Pi >

“Pi: Pi.”

Britannica.com.

< https://www.britannica.com/science/pi-mathematics >

“Pi: A Brief History of Pi.”

Exploratorium.

< https://www.exploratorium.edu/pi/history-of-pi >

“Pi: The History of the Number Pi.”

BBVA.

< https://www.bbvaopenmind.com/en/science/mathematics/history-of-number-pi/ >

“Pi: What is the Number Pi?”

ScienceNotes.

< https://sciencenotes.org/pi-facts/ >

Strang, Gilbert.

Computational Science and Engineering.

Wellesley, MA: Wellesley Cambridge Press, 2007.

Strang, Gilbert.

Introduction to Linear Algebra.

wellesley-cambridge press, 2003.

“The Method of Undetermined Coefficients.”

MIT OCW.

< https://www.youtube.com/watch?v=mKYlNJhK_2o >

“The Simple Math Behind the Mighty Roots of Unity.”

QuantaMagazine.

< https://www.quantamagazine.org/the-simple-math-behind-the-mighty-roots-of-unity-20210923/ >

Wolfram Research Inc.

Mathematica.

< https://wolfram.com >

“Zero: Bible Meanings, Zero in the Bible.”

BibleMeanings.

< https://biblemeanings.net/number-0-meaning-in-the-bible/ >

“Zero: Division by Zero.”

Brilliant.org.

< https://brilliant.org/wiki/division-by-zero/ >

“Zero: Division by Zero—Definitions, Examples, Facts, FAQS.

SplashLearn.

< https://www.splashlearn.com/math-vocabulary/division-by-zero >

“Zero: Properties of Identity, Inverses, and Zero.”

LibreTexts.

< https://math.libretexts.org/Bookshelves/PreAlgebra/Prealgebra_2e_%28OpenStax%29/07%3A_The_Properties_of_Real_Numbers/7.05%3A_Properties_of_Identity_Inverses_and_Zero >

“Zero: Number Systems with Practical Applications for Division by Zero’

MathStackExchange.com

< https://math.stackexchange.com/questions/4638606/are-there-any-number-systems-with-practical-applications-in-which-division-by-ze >

“Zero: The Profound Significance Of Nbr 0 In The Bible: Unveiling Its Symbolic Meaning.”

ChristianWebsite.com

< https://www.christianwebsite.com/number-0-meaning-in-the-bible/ >

Zero: The Concept of Zero.”

HistoryMath.com.

< https://www.historymath.com/the-concept-of-zero/ >

“Zero: Uncovering the Hidden Nbr 0 Meaning in the Bible.”

BibleMeanings.

< https://biblemeanings.net/number-0-meaning-in-the-bible/ >

“Zero: Why is Zero Called the Additive Identity?”

CK12 Foundation.

< https://www.ck12.org/flexi/math-grade-7/applications-of-properties-of-addition/why-is-zero-called-the-additive-identity/ >

 

Notes

 

[1] The mathematical description of this seed pattern can be given using polar coordinates. Helmut Vogel’s model (1979) describes the position of each seed with the following equations:

 

r[n]=(n)^1/2,​

theta [n]=n phi,

 

where n is the index of the seed,

r is its radial distance from the center,

theta is its angle which runs from 0 to 2 pi,

phi is the golden angle (137.5 degrees) ( pi radians)/(180 degrees) or approximately 2.40 radians (for comparison, half a full circle is pi radians or approximately 3.14 radians), so God’s golden angle is a smidge more than three-quarters of a half circle— in radians we have 2.40/3.14 or about 0.764 to three significant figures (Fig. 9). God grows things goldenly, we mean this literally. The golden angle arises from the division of a circle into two arcs, say {a,b}, according to the golden ratio (~1.618…, itself an irrational number–non-terminating, non-repeating, cannot be expressed as a simple fraction). More specifically, given a circle with a circumference (a + b), where a represents the longer arc and b represents the smaller arc, the golden angle is the angle subtended by the smaller arc b.