Introduction
First some definitions that will become clearer and seem simpler as we go along.
- A mathematical base is simply the number system one is using. It tells you how many digits you’ve got before you need to “roll over” to the next place value. For example, let’s consider the most familiar base to all of humankind—base-10—what we like to call the “finger base.” It uses the digits 0-9, but that is not practical oftentimes for counting (I’m still looking for my zeroth finger), the digits 1-10 are more natural and user friendly most often, so we will describe it like that. Counting, that’s how it all started—counting stuff from 1 to 10 until you’ve got to “roll over” to 11, maybe using ten fingers and one toe! No, actually, one would count up to 10 with the “fingers-placeholder” in mind, then one would remember that an entire 1-10 base-10 stretch has taken place and one would use the first finger again as a 1 whilst remembering that previous stretch of 10, and in your head you just reckon it to be 10+1=11, and on it goes with every “full house” of 10. With every full house of 10, stuff needs to roll over to open the door of an empty “10s house” and fill it up too, and on and on it goes like that adding stuff up as intermediate steps. So that’s our familiar base-10, it’s clearly rooted in the human anatomy this here “finger base;” it came about by counting on our ten fingers, and its simplicity makes it fundamental for basic arithmetic and everyday calculations like commerce and measurement and whatnot, and it goes without saying that it was foundational to primitive mathematics. On the other hand (not literally), the natural base, i.e., E, is intrinsically tied to exponential growth, rates of change, and phenomena such as compound interest, population dynamics, and radioactive decay. Its significance arises from its robust mathematical properties, like its derivative[1] and its integral[2] being proportional to itself. How did the Creator manage, let’s say, population growth? The overarching trait He encoded into it is that incremental changes in a given population depend on the current state of that population–not really a mind bender here but nevertheless, does that sound familiar from what was just said about E’s derivative being proportional to itself? Who thought of that, how, and why? And how was it put into practice on such a universal scale–the universe defaults to E-based growth hands down? It’s so simple on the surface this growth trait, it’s exactly what one would expect, but wow, to put that into practice harmoniously on a universal scale takes a little something else to put it mildly. One must have a thoroughly circumspect view of the universe to do that aright else population after population would either “explode” into who knows what, or disappear altogether. Well, traits such as this make E essential in calculus and modeling continuous change—mathematical enterprises that mark a profound leap forward in humankind’s computational savvy. So how did it happen that humankind “found” this strange base-E? Our Creator, the Agent of Creation, even Jesus, led us to it (mustard seeds growing, the lilies of the field, Matthew 6:28-29, 13:31-32 metaphorically resonate with exponential growth and natural patterns, however, these are symbolic teachings rather than mathematical principles). So how Did Jesus actually reveal it to us? He revealed it to us through His servants as pointed out in a moment. He revealed it to us, fallen, out of graciousness and lovingkindness, to help us out with our computations and attendant manifest societal progress, which is largely gated by how well we compute. Something interesting happened as humankind began to think more and more computationally: base-E emerged. Its discovery was driven by a sore need to understand continuous growth and a keen desire to understand compound interest (this dynamic visionary duo—need and desire—drives innovation). The Christian mathematicians Jacob Bernoulli and Leonard Euler formalized its properties while exploring limits as compounding periods approached infinity (infinity, now there’s a concept). And base E naturally emerges when considering a particularly interesting limit, a limit that captures the essence of continuous compounding (Fig. 1, this is the genius of Bernoulli). Euler further connected it to brother John Napier‘s logarithms, to differential equations, and to its transcendental nature; he also gave it its name, i.e., “E.” But more specifically, why is Bernoulli’s limit so remarkable? The term 1/ x approaches 0 as x grows infinitely large, making (1 +1/x) approach 1, however, when this “1-approaching” expression is raised to exponentially larger powers, then the whole thing, i.e., (1 +1/x)^x, “explodes” juuust enough to converge precisely to Euler’s number E (=2.718…)! Wow, who could have thought of such a clever and elegant mechanism as this, and encoded it into the entire universe? This limit’s unique behavior landing on E forms the backbone of fundamental relationships in mathematics, including the elegant equation that brings together the dream team of numbers {i, 0, 1, E, Pi} (Euler’s identity). Truly remarkable, isn’t it? The interplay between infinitesimally small increments (the 1/x contribution) and compounding large powers (the exponent x contribution) as per Bernoulli’s limit captures the mechanics of continuous growth observed in natural phenomena like population growth, radioactive decay, and financial compounding and more. But this limit looks a little strange, does it not (Fig. 1)? Indeed, but while the limit may seem esoteric due to involving infinite processes, its underlying mechanics reveal profound connections in mathematics and nature. Ultimately, the limit’s beauty lies in how it bridges simplicity (adding and raising powers) and profundity (revealing E, the transcendental number governing myriad natural laws), and not least it shows how mathematics can uncover “hidden” structures in the universe. Let’s zoom back out to the level of the bases—together, these most common and most used bases (10, E) frame the fusion of practicality and mathematical elegance that anchors much of human endeavor, from simple counting, measuring, and commerce, to advanced biological and physical science. In short, these two bases one over against the other bespeak an interplay between intuition (base-10) and abstraction (base-E), reflecting the trajectory of human thought that got us where we are today by God’s exceeding grace—a highly abstraction-oriented civilization of peoples built on a firm foundation of “finger-intuition.”
- A mathematical sequence is an ordered list of things. For example, {2, 4, 6} is a mathematical sequence because it follows a clear arithmetic pattern where each term increases by a constant difference of 2; in fact, this is an arithmetic progression. But the word “ordered” in the context of sequences can be a little tricky, it literally means that the arrangement of elements matters, not necessarily that there’s a sequential or predictable pattern to the numbers. Consider {1, 9, 7}–this is still an ordered sequence, even though it lacks a recognizable progression or rule. The fact that changing the order, e.g., to {9, 7, 1}, creates a different sequence confirms that the original order is significant. So, “ordered” means the specific placement of elements, but it doesn’t imply that those elements must follow a rule like arithmetic or geometric progressions.
A mathematical series adds the terms of a sequence together, for example given the mathematical sequence {2, 4, 6, …}, we get the mathematical series 2+4+6+… - Logarithms are the genius of the Christian mathematician John Napier. They are intrinsic to the relationship between powers of a base and the operations that reverse them—bottom line, logarithms and exponentiation are inverse operations. In practice, practically, a logarithm is the power | exponent to which a given base must be raised to equal some value. For example, 10^3=1000, hence Log[base-10,1000]=3. Aside, problems that end up having uncommon bases are commonplace, and one of the handiest log tools is the “change of base formula,” like so: Log[base-b,x]= Log[base-c,x]/Log[base-c,b], e.g., Log[base-6,48] can be shifted to base-10 so: Log[base-10,48]/Log[base-10,6]=2.161 rounded—it’s a dandy…
- A transcendental number is a number that cannot be expressed as the root of any non-zero polynomial with rational coefficients–let’s make that a little more palatable[3]. This property places transcendental E beyond algebraic numbers betraying its deep connection to non-algebraic structures in mathematics. Its transcendence makes intelligible its unique role in calculus, complex analysis, and natural systems, where its value emerges intrinsically rather than through algebraic construction. (It, like transcendental Pi, is not a human concoction, but rather a discovery, a revelation; it existed before we humans were computing; we should tuck that away and plumb the depths.) The literal term “transcendent” is chosen because it reflects the idea of going “beyond” or “surpassing” the limits of a certain framework; in mathematics, transcendental numbers like E are named as such because they go beyond the set of algebraic numbers—they cannot be the root of any nonzero polynomial equation with rational coefficients. The word captures the concept of E’ s nature exceeding the bounds of algebraic structures, thus squarely situating it in the realm of deeper and more abstract mathematical properties. It is a fitting term to describe this number that plays such a fundamental role in continuous growth, change, and myriad natural phenomena.
One-Half Power Roots of Ten
Referring to figure 2, the # exponent on the 2 in the Array function is an iterator which we will replace with “x” in the discussions to make things less esoteric and the reader can disregard the Array function altogether and just concentrate on the sequence of numbers it produces, which we are calling “roots10,” because they are roots of base-10. Looking at the roots10 sequence of figure 2, what do you notice? What really interests us is the fractional part (it comes after the decimal point)—it is all over the map and thus hard to compare from one member of the roots10 sequence to another, so we are going to fix all that because we are going to work with roots10 a lot and will explain it in more detail as we go along. Now roots10 was generated by raising base-10 to successive one-half powers—10^(1/(2^x))—to get a sequence of base-10 roots; for example the 3.16228 in the sequence is the square root of 10 which is the same as 10^(1/2), and 1.77828 is the fourth root of 10, which is the same as 10^(1/4), and so on. Essentially, the roots10 pattern is {10^(1/2), 10^(1/4), 10^(1/8), 10^(1/16)…} (note that if the divisor changed to say 1/3 as in roots10 = Array[10^(1/3^#)&,10], then the roots would look different and the rate of convergence would be different for sure, but, the end result that we will expound on below would be the same–just an interesting side note before we get started). So, figure 2 shows successive one-half power roots of 10 which we will be working with throughout.
Differences Hinting at Convergence
Next, we are going to look at the differences between the roots of our unconditioned roots10 sequence (figure 3). Notice how the differences are halving later in the sequence. It unambiguously tells us that this sequence of successive one-half power roots of 10 is converging toward something, something mathematically quite natural, and we are very interested in finding out what that something is. That convergence, understanding it, is one of our main goals in this study.
Conditioning the Roots10 Sequence
(Updated 04/02/25 to include derivative-like behavior coming from small exponential changes.) Taking another look at the roots10 sequence (figure 2), it is clear that as x increases, the roots10 generator 10^(1/2^x) decreases, it decreases from 10^(1/2)=3.16228–>10^0=1, as x goes from 1–>infinity. Since we are going to be looking closely at the change between the roots, and how that change diminishes further out in the sequence–because convergence requires that change to zero out–we are going to strip the generator of that red font 1 (it’s worth repeating, that 1 shows up further out in the sequence where all the interesting convergence action happens), so that the only thing generated by our roots generator is bare change from that 1. So our first conditioning step is to remove that 1 which essentially is like a downward offset, it just shifts the entire generator output downward so as to be able to better resolve change relative to 1, and we will do it like so: 10^(1/2^x)-1. This will allow us to focus singularly on the diminishing change from 1 as x grows without having that 1 in the mix further out in the sequence dominating the output (say again, further out in the sequence is where all the interesting convergence action happens, and, where all the roots are extremely close to 1, sort of “sitting on top of one another” way out there). Stripping away that 1 is like a resolution step, a downward shift toward 0, which makes those tiny changes out yonder that are barely greater than 1 stand out by moving them away from 1; it makes these tiny differences “look bigger” because it (the 1) is not present to “tower over” them, it removes a sort of “masking effect” imposed by the 1. Here is an example to make this clearer. Consider these arbitrary numbers each of which is really close to 1:
{1.00001, 0.99998, 1.00011, 0.99994, 1.00012}.
Now strip the 1 away, we get this:
{0.00001, -0.00002, 0.00011, -0.00006, 0.00012}.
These are deviations from 1. But notice how really tiny they are–that is precisely what is happening to the roots10 sequence the larger x gets (except there are no numbers less than 1, they are all greater than 1, but barely so), i.e., the further out we are in the sequence those deviations from 1 are almost imperceptible even within the numerical precision of our computers. So the first step–stripping the 1–shows the deviations very clearly, and if the sequence is to converge, then ideally they need to diminish altogether–they need to zero out–all zeroes (the numerical precision of our computers comes into play here, and we have to convince ourselves that accepting what is practical, rather than ideal, is acceptable, which it is for this simple problem). Looking at the stripped down generator: 10^(1/2^x)-1, it is clear that as x grows now, that whole thing will tend toward 0–we have shifted it from a baseline of 1 at large x to a baseline of 0 at large x–this is good because that exposes zero-concentric (exceedingly tiny) deviations really well, especially those far out in the sequence where all the interesting convergence action happens. But they are going to be very tiny at large x, making it difficult to register meaningful relative change, even within the numerical precision of our computers, so we will also put a “magnifying glass” into the stripped-down generator, and the best way to do that is to use the generator’s exponent itself as a divisor–recall that divisors whose value is less than 1 “magnify” their numerator in proportion to the degree by which the divisor is less than 1. Let’s see what happens to our deviations example when we do that. Here are the deviations “magnified” by 1000 which is the same as a division by 0.001–even though the values have changed to get the better resolution, they have all changed in lockstep, consistently, and all have the same baseline:
{0.01, -0.02, 0.11, -0.06, 0.12}
This is where our example departs from the roots10 generator conditioning we will do because of the significant difference in the divisors utilized and what that implies as concerns the baseline and derivative-like behavior in our roots generator; what we have done here is just an example to set up our roots10 generator conditioning discussion.
The thing is, as our generator’s exponent gets really tiny at large x way out in the sequence, so will the deviations divisor if we use that exponent to do the division, thus not only scaling the deviations just right so that they don’t get conflated to 0 by the computer, but maintaining precisely 1 as the baseline–that’s the big difference to the example above where we just sort of eyeballed the output and intuitively chose a (constant) divisor of 0.001. So, we divide our 1-stripped generator, i.e., 10^(1/2^x)-1, by its variable exponent, by (1/2^x), because this divisor’s “exceeding smallness” at large x will serve us well here. But there is more to this division than mere “magnification,” our conditioned roots generator resembles the form of a derivative in the limit as the divisor (1/2^x)–> 0 at large x. This creates a bridge between discrete changes in the generator function and its continuous growth rate. In this way, it comes as no surprise that the sequence manifested by the conditioned roots generator converges to the same proportionality constant (Log[base-E,10]=2.3026) that taking the derivative of 10^x does (d[10^x]/dx=Log[base-E,10] 10^x).
By stripping the 1 toward which the sequence tends at large x (10^0), per step 1, and magnifying the very tiny consequential deviations per that strip at large x, which are relative to baseline 1, we will realize in the magnified deviations a sort of “growth change factor” relative to 1. Even though we stripped away the 1, it is in a sense an “artificial” strip, it just shifted the baseline–the real “growth change factor” is really/actually relative to 1 (like the deviations in our example, they are relative to the stripped 1 there too and not to the artificial/shifted-to 0 baseline). Figure 4 shows the conditioning steps put together—the subtraction of 1 and division by (1/(2^x)—and what we see in the figure is that the sequence converges to the “natural” logarithm of 10 (Log[base-E,10]=2.3026 rounded). The sequence converges to Log[base-E,10] because the process of conditioning, of “noise removal,” reveals the intrinsic relationship between exponential and logarithmic functions. By subtracting 1 and normalizing by (1/2^x), we isolated the core exponential behavior of the sequence, exposing how small exponential changes (via 1/2^x) translate into logarithmic scaling. This scaling reflects derivative-like behavior, i.e., it reflects the logarithmic rate (“rate” is a cozy way to say the more fancy “derivative”) of growth inherent in the base-10 exponential generator function—to put it more picturesquely, it is a precise measure of “how hard” the tiny exponential changes are driving the sequence’s behavior. (Note again that the derivative of 10^x=Log[E,10] 10^x, so both the derivative and our sequence manifest the Log[E,10] proportionality constant that keeps exponential changes consistent with the current state of growth–that red font verbiage is a universal property of exponential functions no matter what the base is, and that constraint is being met here plain as day; e.g., for any exponential function, say, base^x, its derivative is proportional to the function itself: d[base^x]/dx=Log[E,base] base^x where base^x is the function itself.) This property is what makes exponential growth/decay so very special; our Creator’s genius shines here–and He actually put it into practice, and it flat works, everywhere: in our bodies, our universe, everywhere. Yet, at the same time, Log[base-E,10] also acts as a base-10 to base-E conversion multiplier–these two roles are inherently linked because both base-E and base-10 logarithms are just different expressions of the same exponential-logarithmic interplay (base-E and base-10 logarithms are like different “dialects” of the same exponential-logarithmic language; exponentials and logarithms are fundamentally inverse operations, two sides of the same coin; it follows that all exponentials and logarithms share the same universal structure).
But by way of this conditioning we have set ourselves up for some possible math trouble. If 10^(1/2^x) approaches 10^0= 1 with increasing x, then 10^(1/2^x)-1 approaches 0, and if the divisor (1/2^x) approaches 0 with increasing x, then we have an indeterminate form 0/0 in the limit as x approaches infinity? Indeed, but as will be pointed out later, the rate of convergence of this conditioned sequence is hyper-fast, so after only a few iterations–some 15-16, a far cry from infinitely many–it flat nails the convergence limit, so we are going to escape getting burned here by indeterminate forms because we will not have to take it to said limit (going to the limit, if that were possible, would force us to call on L’Hopital’s Rule to try to make sense of the indeterminate form). And lo and behold something interesting happens when we perform these sort of conditioning “cleanup” steps—it creates a decreasing sequence of roots that fast converges toward a limit, which is itself a value that is proportional to the “rate of change” inherent in the sequence at these tiny exponent values. Why do we say, “proportional to the rate of change?” For a sequence to converge to a specific value, the differences between consecutive terms must decrease over time (consecutive deviations from 1 in our case), indicating a diminishing rate of change (less and less change), and for this setup, the change between consecutive terms (relative deviations from 1) is approaching nil hyper-fast such that within the numerical precision inherent in our computer crunching the numbers, it (the hardware/software) essentially”sees” convergence after only 15-16 iterations. So, in general, this diminishing rate of change behavior ensures that the sequence approaches a limiting value as the number of terms increases. In short, the change between successive roots (relative deviations from 1) is becoming exceedingly smaller, much like a derivative approaches 0 (slope flattens) as it approaches a critical point, and in this case, the “growing decrease” in the change between the roots in the conditioned sequence tells us that the terms are stabilizing and “locking in” on a particular limit. The decrease and convergence also means that the “distance” between the terms of the sequence and the limit toward which they converge is shrinking (not just from term to term, but from each term to the limit)—it is as if one is zooming in on the limit with each successive iteration/term, and this “zooming behavior” is a hallmark of stability and convergence in numerical sequences and, importantly, in nature, when described by such a sequence. therefore, per figure 4 we see the conditioned roots10 sequence “settle down” toward its natural logarithmic destination of 2.3026. (Again, after around 15-16 iterations, the output stabilizes as shown because the terms are so close to the actual Log[10] limit that further increases in x produce negligible differences; this “locking in” happens due to the nature of exponential and logarithmic convergence—the computations are effectively observing the infinite limit within the bounds of numerical precision afforded by the software and hardware doing the computing; and a mere 15-16 iterations never “see” the indeterminate 0/0 that must arise and be settled via L’Hopital’s Rule if x were to somehow actually approach infinity bottom line.)
Other bases (positive, and greater than 1), undergoing a similar exercise as just performed on base-10, similarly converge to their natural logarithm, which is the conversion factor to the Creator’s ubiquitous exponential reality in those bases (more on this conversion factor in a moment). These natural logarithms, i.e., the aforementioned proportionality constants, essentially measure the growth rate relative to the base-E, so all bases behave similarly when conditioned this way—the thing that remains constant and is converged to, in all cases, is a function of the natural, universal, base-E—that’s the key point. It is intuitively obvious therefore that base-E is a unifying base—it is in that sense a sort of “linga franca for bases,” or “bridge base” to the universe’s myriad numerical expressions. We should already suspect this role from how it connects the most important non-physical constants in the created order—the dream team of numbers: E^(i Pi)+1=0 (Euler’s identity, arguably the most celebrated gem in mathematics).
What does it all mean, what good is to be gained from this 2.3026 convergence limit, practically? It is the multiplier of the powers of 10, i.e., base-10 logarithms (so-called common logarithms per Henry Briggs), that converts them to the natural (base-E) logarithms—that’s a big deal because base-E is the universal base, it is the Creator’s growth-scale standard in our estimation, and it “popped out” of this seemingly totally unrelated conditioning exercise centered on a totally unrelated “finger base” no less, base-10. And this limit’s inverse goes in the other direction, that is, 1/2.3026 (approximately 0.4343) is the multiplier that converts natural logarithms (base-E) into base-10 logarithms.
Let’s kick the tires and try it out. What is Log[base-10,10]? The question is asking what is the logarithm base-10 of 10? We must raise 10 to power 1 to nail 10, i.e., 10^1=10, therefore, Log[base-10,10]=1. Now let’s kick the tires: what is Log[base-E,10]? The question is asking for the natural logarithm of 10. According to the recipe, the answer is 1 times the conversion multiplier of 2.3026 = 2.3026, which is precisely the natural logarithim of 10. Now the inverse: knowing that the natural logarithm of 10 = 2.3026, i.e., Log[base-E,10]=2.3026, how do we convert that to the common logarithm of 10, that is, to the base-10 logarithm of 10? We are after Log[base-10,10] given Log[base-E,10]. Following the recipe we use the inverse of the multiplier (1/2.3026) times Log[base-E,10] = (1/2.3026) times 2.3026= 1; the answer is precisely 1, which is in fact Log[base-10,10]. So that’s an example of the inverse conversion from (natural) Base-E to (common) base-10. Actually, this conditioning exercise gives us insight into how to handle base-whatever to natural Base-E and vice versa conversions: if working with a base other than base-10, we use the natural logarithm of that base as the conversion multiplier. For example, converting to and from base 2 involves using the natural logarithm of base-2 (approximately 0.693, Fig. 4a and its inverse (1/0.693).
Cutting to the chase with Higher Math
Everything we have done so far could have been shown by this simple line of code (figure 5). But we wanted to fill in the gaps for clarity and to show how the mathematics unambiguously gets us from the finger-base logarithm of 10= 1, to the real deal natural logarithm of 10 = 1 times 2.3026.
In figure 6 we are not adding anything new to what has been done, we are simply looking at it from another perspective–note what happens in the limit as the iterator x gets huge—we show it approaching infinity in the figure, and again everything we have done so far could have been presented as this one simple and elegant line of code. Unlike finite iterative evaluation as before (Fig.4), evaluating the sequence to infinity here inherently involves addressing the indeterminate form (0/0), thus the computing software would rely on L’Hopital’s rule or equivalent symbolic method to resolve it rigorously and determine the precise theoretical limit.
Now let’s get yet another perspective, let’s do a rewrite of our roots10 generator in terms of the natural log and exponential function because then the sequence isn’t tied specifically to base-10 anymore, thus making it clear that similar behavior would occur for other bases as well as mentioned above, and as noted in the introduction, the exponent can be anything that has a 1/x nature. Recasting the sequence in terms of logarithmic and exponential forms links it to derivative-like behavior and other mathematical structures, so in short the following rewrite is not just a computational tool, it provides deeper insight into why the sequence converges to the natural logarithm of 10, i.e., 2.3026, and so it reveals the universality of the result and bridges the gap between sequences and their continuous counterparts. Here is our conditioned roots10 generator again:
(10^(1/2^x)-1)/(1/2^x) (cf. Fig. 4). It could be rewritten more generally as:
x (10^(1/x)-1),
which is the same as:
x (E^(Log[E,10]/x)-1),
and now if we expand this more general form as a Taylor series as x gets very large, we get the result of figure 7. Notice the sum—this is clearly a mathematical series by definition. The first term shown in the figure (Log[10]) is understood to be the natural logarithm of 10, which is precisely the 2.3026 limit to which the conditioned sequence converges, and the second term: (Log[10]^2)/(2 x), reflects the fast rate (mentioned in the conditioning section) at which the generalized sequence approaches said limit, thus giving additional detail about the approximation for large but finite values of the iterator x; the smaller this second term, the faster the convergence, hence we want a small, preferably constant numerator and large, growing denominator for hyper-fast convergence, and the higher order terms including the second term clearly become negligible as x grows, thus the series “locks in” on the leading Log[10] term which dominates the series at very large x. So we have shown convergence to Log[base-E,10] again, this time circumventing base-10 in the setup to highlight the universality of this Log[base-E,10] and more generally, that the natural logarithm per se serves as a universal translator across bases and systems.
It’s a bit of overkill all these perspectives but hopefully adds some clarity and persuasion as to base-E’s universality, and not least its “existence” solely on a mathematical basis (and recall Bernoulli’s limit is in the mix here Fig. 1). The mathematics clearly predicts this existence, and then we see it in nature all over the place as a sort of growth-scale standard. Plato would (probably) argue for the eternality of its existence per his Theory of Forms, and in fact its existence in math-space would be why he is right. We would argue for the eternality of the mind behind its eternal existence in math-space let alone its manifest utility and ubiquity in physical-space.
Concluding Comments
Human computing started out with finger-math, it started crudely with base-10, the centuries-old “finger-base.” And then came finally in the seventeenth century logarithms per John Napier. Napier’s logarithms were eventually refined by the highly influential Christian mathematician Henry Briggs, who introduced common logarithms (base-10) for practical use. Napier’s work laid the foundation for logarithmic systems no question, and Briggs refined it, and the quintessential logarithm, the natural logarithm (and its connection to E), was developed upon these groundbreaking contributions to this mathematical field of study (roughly one-hundred years passed between Napier and Briggs’ work and the formal development of the natural logarithm and its link to E).
Base-10 is not natural, base-10 “artificially” arose because we humans have ten fingers to count with and add with, but it simply is not mathematically natural and pure this finger-base, not like base-E. What we did above showed that by stripping the roots10 sequence of 1, namely 10^0 at large x far out in the sequence, and by normalizing the resultant deviations from 1 by the generator’s power–that is why we divided by the root power (1/2^x) above (normalization magnified the output, embedded the derivative-like behavior inherent in the divisor–>0 at large x, and ensured that the sequence doesn’t grow disproportionately; disproportionate growth breaks the fundamental rule that exponential growth is always consistent with the current state)–there emerged a convergence toward a certain number, the natural logarithm of 10, of the very base-10 we were working with (Log[base-E,10]=2.3026), consistent with the derivative d[10^x]/dx=Log[base-E,10] 10^x. And that result we use to multiply base-10 logarithms to shift them away from artificial and toward natural, toward what is called base-E, which is a natural, pure, and fundamental base, a universal base even, independent of fingers for counting and so on. And we know from our study of the natural world through various avenues of inquiry across the centuries that Base-E is hands-down the “universe’s base,” the universe “expresses itself” in base-E, and so for that very reason base-E is called the “natural” base, because it is ubiquitous, it shows up literally everywhere in nature. And it follows that the logarithms related to Base-E are similarly called “natural,” natural logarithms in that case. Recall that a logarithm is the power required to raise a base to a certain value, e.g., we raise base-10 to power 3 to nail 1000, so, Log[base-10,1000]=3—10x10x10=10^3=1000; as another example particular to our context, we raise base-E to 2.3026 to nail 10 (E^2.3026=10), so, Log[base-E,10]=2.3026. The reader can see how clever use of logarithms and their related base allows one to nail any (positive, real) number, so even though Napier, Bernoulli, Euler and others were working with logarithms as discussed above, the whole number line is actually in view.
Now just as Pi is a natural number representing the circumference divided by the diameter of any circle, and shows up as a root in all manner of periodic problems, so too E is a natural number, and it naturally shows up in counting and adding and multiplying and exponentiating—in short it shows up as a root in growth scenarios be it positive or negative growth at hand. If you will, think for a moment about the physical patterns of the world around you beloved reader—they are largely driven by four natural mechanisms, and E and Pi are fundamental to each—from the simplest to the most complex we have these four: uniformity, repetition, nesting, and randomness/complexity (Wolfram NKS, passim). Base-E thrives in processes associated with uniformity and repetition, yet it also connects deeply to complexity, as follows:
- Uniformity: E models continuous growth, like compound interest or exponential decay, where the process behaves uniformly over time.
- Repetition: E shows up in scenarios involving repeated, compounding actions, such as slicing time into ever-smaller pieces in calculus.
- Randomness/Complexity: E plays a role in probability and natural phenomena, where complex patterns arise from seemingly random processes (e.g., in statistics | stochastic growth, which is growth that incorporates randomness or unpredictability, commonly used to describe phenomena where outcomes are influenced by both predictable trends and random variables).
Now as for Pi, it is rooted in nesting and randomness/complexity, and it clearly has connections to repetition, as follows:
- Nesting: Think of Pi in geometry—circles and spheres have nested relationships, and Pi defines their ratios and areas, creating layers of interconnectedness.
- Repetition: Pi is intimately tied to periodicity and wave patterns, like the repeating cycles of sine and cosine in trigonometry describing oscillations and rhythms.
- Randomness/Complexity: Pi emerges in chaotic systems and random distributions, like Buffon’s Needle problem or the randomness found in its own digits.
In short, E leans toward processes involving smooth, continuous growth or change, while Pi resonates with cycles, patterns, and the intricate interplay of geometry and randomness.
E is real, it truly is the one and only natural base, hence we find it encoded into our universe literally everywhere. E as the universal base undeniably acts as a kind of growth-scale standard in the mathematical architecture of the universe. Its presence in exponential growth | decay, compounding, and countless natural and physical processes isn’t arbitrary, it is intrinsic, and this alone suggests that E isn’t just a mathematical convenience—it is a foundational “scale” woven into the very fabric of reality.
From a theological standpoint, E can rightly be seen as a “measure” of the harmony and order anchoring nature. It is almost as if the processes of growth and change/transformation per se have been calibrated to follow this E-scale, this growth-scale standard, whether in biology (e.g. population growth), physics (e.g. radioactive decay), or economics—financial and otherwise (e.g. compound interest [financial], but consider nutrient cycling in organisms, carbon storage in forests). And the universality of E gives the impression that nature is in fact a created order governed by an underlying logic which bespeaks design in the extreme.
It is undeniably awe-inspiring and humbling—the existence of a “natural” base like E seems like a profound mystery at first glance. Why is it there? Why should there even be a natural computing base in the first place? The only logical indeed practical reason is computational design, that seems to make the most sense. There’s flat out no necessity, no cosmic law demanding that such a base must exist, not at all. And yet, there it is, arising inevitably, singularly, from the structure of mathematics itself, as pointed out above, and mathematics is a cerebral game, a thinking mind game, is it not? The strangeness of E existing at all—in the mathematics that predicts it and nature which hand-in-glove embodies it—should lead us to the Eternal Mind, even Word—that would be Jesus Christ—who spoke a Word of Code, yea, who spoke, and muscled, this here universe of ours into existence, utilizing E as the growth-scale standard in His myriad encoding processes that comprise His elegant exponential framework (John 1:1-3).
Praised be your Name Eternal Word Jesus. Amen.
Illustrations and Tables
Figure 1. Bernoulli’s limit.
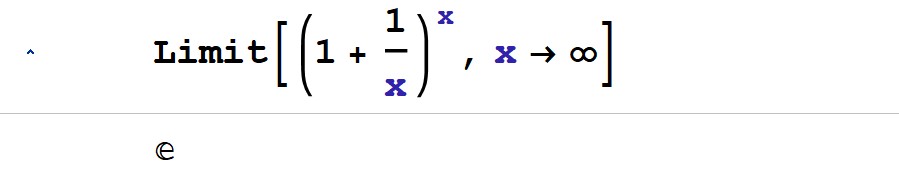
Figure 2. The roots10 sequence.
Figure 3. Roots10 differences.
Figure 4. Strip 10^0=1 and normalize/scale the roots generator; note the diminishing relative change.
Figure 4a. Strip 2^0=1 and normalize/scale the roots generator: convergence is to its natural log–Log[base-E,2].
Figure 5 The natural log of 10.
Figure 6 The conditioned roots10 generator in the limit of large iterator x.
Figure 7. The conditioned roots10 generator generalized, expanded about xo=infinity.
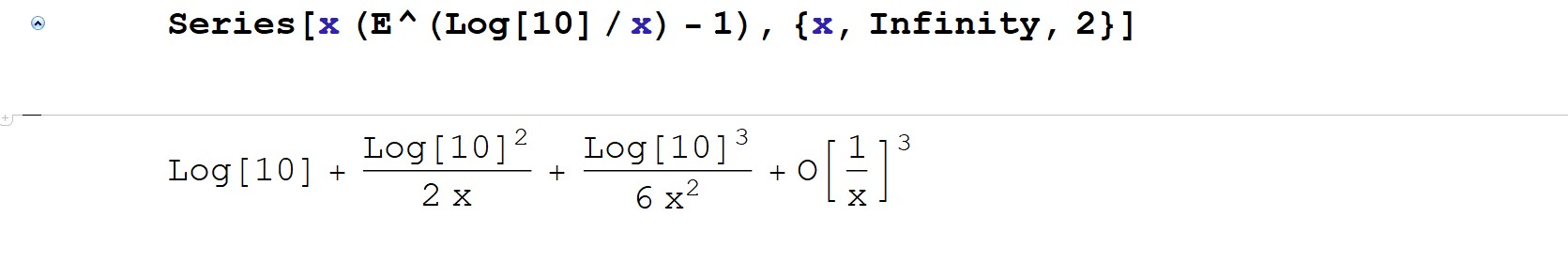
Works Cited and References
“A Letter of Invitation.”
Jesus, Amen.
< https://development.jesusamen.org/a-letter-of-invitation-2/ >
Microsoft, Copilot.
March, 2025.
“The Dream Team of Numbers.”
Jesus, Amen.
< https://development.jesusamen.org/the-dream-team-of-numbers/ >
Wolfram Research, inc.
Mathematica.
Wolfram, Stephen.
A New Kind of Science.
Wolfram Media, 2002.
< https://www.wolframscience.com/nks/ >
Notes
[1] Very loosely put, a derivative can be seen as a deconvolution, i.e., “breaking down” a function by examining how it changes at every point.
[2] Very loosely put, an integral can be seen as a convolution, i.e., gathering information and adding up all the little contributions over a range.
[3] The root (solution) of a non-zero polynomial (at least one nonzero coefficient) with rational coefficients (fractional or integer values multiplying the variables) is a value (let’s call it r) that satisfies/solves the polynomial equation, meaning that when 𝑟 is substituted into the polynomial, the result = 0. For example, numbers like Sqrt[2] or 3/5 are algebraic, because they satisfy/solve the polynomial equations x^2-2=0 and 5x-3=0, respectively, but transcendental numbers, like E or Pi, don’t satisfy any such polynomial equations, they are “beyond algebraic,” hence the term “transcendental.” Transcendental numbers are quite “strange” and fascinating in that respect. Unlike algebraic numbers, which neatly solve polynomial equations with rational coefficients, transcendental numbers completely defy that framework. Their existence shows us that mathematics goes far beyond just algebra—there’s an infinite, mysterious realm of numbers that don’t fit into our usual patterns…
[4] Even though the fractional parts seem scattered, roots10 is still considered a strict mathematical sequence because its terms are ordered. A mathematical sequence doesn’t require “sequential” or smooth changes; it only needs an arrangement of terms following a rule or pattern, which came by way of the Array function here.