Introduction
We are going to start with a short and light technical presentation of the subject, and then straightaway consider our Creator’s hand in it.
What drives the tendency for high concentrations of something in a medium to flux toward ever lower concentrations? Let’s consider two different scenarios,
(a) a drop of ink in water (Fig. 1—gravity is acting, but not involved in the diffusion),
(b) a heated, heat conducting material surrounded by a cool medium: Figs. 2—thin disk, 3—thin disk—notice the initial condition of figure 2 coded in at radius=1, 4—thin disk, 5—thin disk, 6—heated plate—the latter is a video, across the top are monitors of time elapsed in seconds, avg. Tcool, avg. Twarm, T[15,15]=plate middle, where T stands for temperature. The code resets when avg. Tcool and avg. Twarm over the entire grid equilibrate, where the grid consists of the heated plate shown in red (T=1) and its surroundings shown in green (T=0). Time to reset is about three minutes. (The quantification controls on the left are inaccessible, they were originally coded up to demonstrate the utility of discrete feedback in quantifying complex systems, which is outside the scope of this study. You will notice a green sometimes white pointer, at the outset we “parked” it too high, it is not pointing to anything meaningful at the outset; after about 95 seconds it moves down to the monitors and points out things for your eye to follow after that, apologies. After having viewed the video the reader’s eye should be acclimated properly as to the top monitors location.)
In either case (a) or (b) above, something is causing a flow, a flow of atoms and molecules in (a), and heat in (b). Energy is that “something.” In the case of the ink drop it is chemical (potential) energy, in the case of the hot material it is heat energy. Key factors involved in either case, in easy to understand, nontechnical terms, are heat affinity (is the thing a heat “lover”—takes in heat, or a heat “hater”—gives away heat), and temperature, and the degree of the thing’s disorder. Heat affinity, temperature, and disorder. These factors are tabulated for many materials and combinations of materials, and so one can get good insight as to the spontaneity of the flow. The flow itself is described so in (1) simple language, and (2) in more technical language, respectively:
(1) A source causes, i.e., sets up a flow field—a region in which something is flowing.
(2) Mathematically, (1) is the divergence of the gradient (= the Laplacian, a multi-directional, “change in the change” operator that bespeaks curvature in general, and more specifically, it computes a difference based on neighborhood averages).
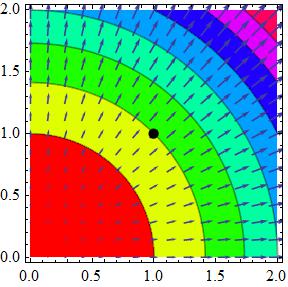
(This section was updated 03/22/2023, A.s.) Looking at the terms individually, “divergence” has precise mathematical meaning, but bottom line, when there is a divergence, there is a source (or sink). And gradient also has precise mathematical meaning—let us ease into it with an everyday example. Motion is some change in position with respect to time, for example, “five miles per hour” in a given direction, i.e., some velocity. Mathematically, this velocity, this motion, is a (one dimensional—1D) first derivative in position with respect to time. In simple words, a derivative is change, be it in position, or in concentration as concerns us in this study. This derivative, this change operator, may be with respect to time, or with respect to some parameter. “Doing a derivative” is how one “writes” the word “change,” mathematically. When one considers motion (change in position with respect to time) in more than one direction, this is tantamount to motion on a surface, and loosely put, that is a gradient, it is the purely spatial multi-directional counterpart of a 1D first derivative, and it is no less steeped in the concept of change than a 1D derivative. But it tells us more than simple change actually, it is in fact a map of the maximum/steepest slope (=greatest change) at each point on the surface (figure 7 shows an arbitrary gradient field; the arrows track paths of steepest slope; e.g., lined up arrows nearby the dot fast track to either end); please note that slope bespeaks change, and change, is caused. Quantifying that cause is the role of the divergence mentioned above. Mathematically, the divergence operates on the gradient to produce a sum of spatial second derivatives—curvature in the extreme—that can be thought of as little (infinitesimal) balls centered at some point in the material (in it’s flow field), the Laplacian then gives the steepest degree of change, i.e., difference, between the average of all the points in the ball and the point at which the ball is centered (the principle of locality holds, and not least optimization by default at the scale of the infinitesimal), and the flow follows these differences downhill, i.e., along the path of decreasing differences, and it stops when the differences in a given direction no longer decrease (see the next section’s discussion about potentials). But what sustains the computation—what “keeps it going” from point to point? The Laplacian as described operates under negative feedback—that is what drives and sustains the computation until it stops, i.e., encounters non-decreasing differences as explained (the discrete Laplacian of figure 6 is based on these differences under feedback). The divergence of the gradient, i.e., the Laplacian here discussed, shows up just about everywhere in classical and quantum physics, because this universe of ours has been optimized by a Grand Optimizer, even Jehovah Jesus, amen. But why this flow in the first place? The above is “how,” but the question we are interested in for this study is, why?
All Things Tend Toward Disorder Post-Fall
We are going to introduce some technical terms but will try to break it all down in an easy to understand way. We have this very important empirical rule hinted at above:
Creator’s Faithful Rule: {[change in] heat affinity minus (temperature times [change in] disorder)}= energy available to do work, i.e., work that causes (spontaneous) flow.
If this available energy is negative, the flow is spontaneous. That may sound backwards, but it behaves like a potential energy. Explanation: A stretched spring has the potential to do work, e.g., when released from tension it can move a block attached to it, the work that it actually does appears in the form of potential energy, and there are various formulas that determine what the magnitude of that potential energy is in different settings. So there is potential, and potential energy, the former is exactly what it sounds like–the “capacity” to do something, and that “doing” will expend some amount of energy, namely the potential energy, i.e., the manifest energy attending realized potential. Here is the important takeaway, all objects in the universe seek the lowest potential possible for themselves, e.g., balls just love to roll downhill, stretched springs just love to snap back, etc. Potential bespeaks a difference, clearly a stretched spring has varying amounts of potential that correlates to the amount of stretch. Potential energy on the other hand is the energy contained in the potential difference between say a relaxed spring and some amount of stretch. Potential energy, therefore, is a relative term, it depends on where one places the zero reference for one’s potential differences. So, potential is the ability or capacity to do work, potential energy is that work’s manifest energy. Importantly, Jehovah’s universe is coded up such that forces lower an object’s potential (forces are the Creator’s “workhorses” if you will), and therefore objects acted on by forces follow paths of decreasing potential, always. Returning to our rule, if potential energy is a negative quantity, it is so because of the choice of one’s zero reference, the actual energy is what it is, it does not “care” where the zero reference is. But there is a very practical side to this negative potential energy that is consistent with and motivates one’s seemingly arbitrary choice of the zero reference—the required negative nature of the (available) potential energy in this context regarding the above rule and spontaneity betrays an energy loss, it indicates that energy is lost in the way of doing work; some work has to take place to get spontaneous flow (spontaneity does not mean “free”/zero cost). Given this brief setup, let’s look at the above rule a little closer and try to understand it. Please note the minus sign before the parenthesis, we have underlined it because of its importance. Temperature will always be a positive number (measured in Kelvin; it may be large or small, but always positive), and so the parenthesis term, negated by the minus sign, will tend to be a negative number, because our created order tends toward increased disorder (Genesis 3:17, Romans 8:19-23; accursed is the ground…), where an increase in disorder is considered to be positive and a decrease in disorder is considered to be negative. So inside the parenthesis, i.e., temperature (positive) times [change in] disorder (positive), will tend to be positive, but negated by the minus sign it will become negative, and so the back half of the rule will tend to be negative. As to the front half of the rule, some setup. Consider that Jehovah created our universe to seek stability (Genesis 1:1-2, “…and God said…”, 1Corinthians 14:33, Colossians 1:16-17), and lowered total energy—this includes potential and kinetic energy—tends toward stability (a ball rolling downhill is stablest when it comes to rest at the bottom of the hill and rest means zero total energy; a hyper puppy is stablest when sleeping, etc.). The front half of the rule involves (change in) heat, and heat is energy, so the front half of the rule, seeking stability, i.e., lowering its total energy, will tend to be negative. So overall, with both halves of the Creator’s rule coming together, the available energy will tend to be negative, and thus, by design of the Creator, flows of whatever will tend to be downhill spontaneously. A word about the direction, i.e., downhill. The upshot is this: stability (lowered total energy, and dissipative forces stabilize systems) and increased disorder together are responsible for the direction of a flow (downhill), and the rule per se is responsible for its spontaneity. The Creator demands stability in His universe (systems tend toward lower energy), and together with His present curse on it (all things tend toward increased disorder, as corroborated by the second law of thermodynamics), it is inevitable that flows of whatever will be downhill, spontaneously—this is the “why” we seek. (Please note that stability and disorder are in tension here, and thankfully so, for they act as a system of checks and balances one over against the other.) The “how,” i.e., the divergence of the gradient, has no real explanatory power, it is the “why” that fills that role. And finally, there is the matter of spontaneous uphill flows; well, that is not natural, it can happen when it is “doctored up” and coerced to do so, but Jehovah did not code up His universe to operate like that whatsoever.
Praised be your elegant Name great Creator God Jehovah, whom we love and adore. Amen.
Illustrations and Tables
Figure 1. Ink in Water Diffusing | Flowing (credit Jill Burrow, pexels.com).
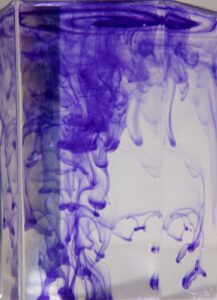
Figure 2. Thin Disk Initial Condition. (No source inside boundary, stream function source [red T=.5, blue T=-.5]], sine series solution.)
Figure 3. Thin Disk Heat Flow. (3D plot of figure 2.)

Figure 4. Thin Disk Halfway Inside. (Polar plot of figure 2.)

Figure 5. Thin Disk Just Inside. (Polar plot of figure 2.)

Figure 6. Preheated Flat Plate. No active source. Feedback solution. Top Monitors: Time, Avg. Tcool, Avg. Twarm, T[15,15] = plate middle.
Figure 7. An Arbitrary Gradient Field. (Gradient arrows everywhere perpendicular to the contours.)
Works Cited and References
“A Letter of Invitation.” (Not cited; may it be a spiritual boon for the beloved reader.)
Jesus, Amen.
< https://development.jesusamen.org/a-letter-of-invitation-2 >
Chad’s Prep: Gibbs Free Energy
YouTube.
“Creation Optimization.”
Jesus, Amen.
< https://development.jesusamen.org/creation-optimization/ >
Dewus, Michael
“2D Heat Diffusion Using a Search, Update, Feedback CA Approach.”
Online Publication, 10-2013.
“Gibbs Free energy.”
Wikipedia.
< Gibbs free energy – Wikipedia >
Wolfram Research, Inc.
Mathematica.